Question

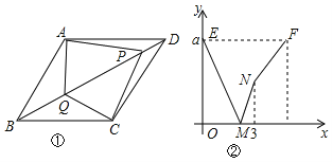
【题目】如图，在平面直角坐标系中，菱形的两条对角线相交于点轴，垂足为点正比例函数的图像与反比例函数的图像相交于两点.

（1）求正比例函数和反比例函数的解析式；

（2）求点的坐标.

Answer 1

【答案】（1）正比例函数:，反比例函数:；（2）

【解析】

（1）根据待定系数法可求得函数解析式；

（2）联立两函数式，可求得A点坐标（-1，-2），设B点坐标（-1，a），根据菱形性质可证得△OAE∽△BAP，根据比例关系可求得a的值，进而得到B点坐标.

（1）∵和经过P（1，2），

∴分别代入得：m=2，n=2，

∴正比例函数：，反比例函数:；

（2）联立 ，解得 或 ，

∴A点坐标为（-1，-2），

设B点坐标为（-1，a），

∵四边形ABCD是菱形，

∴AC⊥BD，

∴∠BPA=∠OEA=90°，

∵∠OAE=∠BAP，

∴△OAE∽△BAP，

∴，即，解得a=3，

∴B点坐标为（-1,3）.