题目内容
已知关于x的方程(m+3)x|m|-2+4m=0①与nx-5=x(3-n)②的解相同,其中方程①是一元一次方程,求代数式(m+x)2014•(-m2n+xn2)+1的值.
考点:同解方程
专题:计算题
分析:由方程①为一元一次方程,求出m的值,代入方程求出方程①的解,即为方程②的解,代入方程②求出n的值,把x,m,n的值代入原式计算即可求出值.
解答:解:∵(m+3)x|m|-2+4m=0①与nx-5=x(3-n)②的解相同,其中方程①是一元一次方程,
∴|m|-2=1,且m+3≠0,
解得:m=3,即方程为6x+12=0,
解得:x=-2,
把x=2代入得:2n-5=2(3-n),
解得:n=
,
则原式=(3-2)2014•(-
-
)+1=-
.
∴|m|-2=1,且m+3≠0,
解得:m=3,即方程为6x+12=0,
解得:x=-2,
把x=2代入得:2n-5=2(3-n),
解得:n=
| 11 |
| 4 |
则原式=(3-2)2014•(-
| 99 |
| 4 |
| 121 |
| 8 |
| 311 |
| 8 |
点评:此题考查了同解方程,解决的关键是能够求解关于x的方程,要正确理解方程解的含义.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
若一个数的算术平方根等于它的本身,这个数是( )
| A、1 | B、0 | C、-1 | D、0或1 |
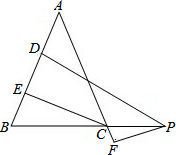 如图,在△ABC中,AB=AC,P为BC延长线上的一点,PD⊥AB,PF⊥AC,CE⊥AB,PD=7,PF=3,则CE=
如图,在△ABC中,AB=AC,P为BC延长线上的一点,PD⊥AB,PF⊥AC,CE⊥AB,PD=7,PF=3,则CE=