ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“―÷Σ≈ΉΈοœΏ![]() Θ®
Θ®![]() ΓΔ
ΓΔ![]() ΈΣ≥Θ ΐΘ©ΒΡΕΞΒψΈΣ
ΈΣ≥Θ ΐΘ©ΒΡΕΞΒψΈΣ![]() Θ§Β»―ϋ÷±Ϋ«»ΐΫ«–Έ
Θ§Β»―ϋ÷±Ϋ«»ΐΫ«–Έ![]() ΒΡΕΞΒψ
ΒΡΕΞΒψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§
Θ§![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§÷±Ϋ«ΕΞΒψ
Θ§÷±Ϋ«ΕΞΒψ![]() ‘ΎΒΎΥΡœσœόΘ°
‘ΎΒΎΥΡœσœόΘ°
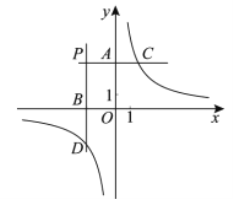
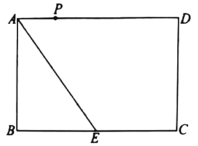
Θ®1Θ©»γΆΦΘ§»τΗΟ≈ΉΈοœΏΨ≠Ιΐ![]() ΓΔ
ΓΔ![]() ΝΫΒψΘ§«σΗΟ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΘΜ
ΝΫΒψΘ§«σΗΟ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΘΜ
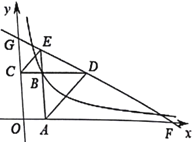
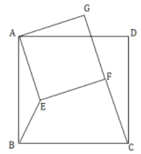
Θ®2Θ©ΤΫ“ΤΘ®1Θ©÷–ΒΡ≈ΉΈοœΏΘ§ ΙΕΞΒψ![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ![]() …œΜ§Ε·Θ§«“”κ
…œΜ§Ε·Θ§«“”κ![]() ΫΜ”ΎΝμ“ΜΒψ
ΫΜ”ΎΝμ“ΜΒψ![]() Θ°
Θ°
ΔΌ»τΒψ![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ![]() œ¬ΖΫΘ§«“ΈΣΤΫ“Τ«ΑΘ®1Θ©÷–ΒΡ≈ΉΈοœΏ…œΒΡΒψΘ§Β±“‘
œ¬ΖΫΘ§«“ΈΣΤΫ“Τ«ΑΘ®1Θ©÷–ΒΡ≈ΉΈοœΏ…œΒΡΒψΘ§Β±“‘![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() »ΐΒψΈΣΕΞΒψΒΡ»ΐΫ«–Έ «Β»―ϋ÷±Ϋ«»ΐΫ«–Έ ±Θ§«σ≥ωΥυ”–ΖϊΚœΧθΦΰΒΡΒψ
»ΐΒψΈΣΕΞΒψΒΡ»ΐΫ«–Έ «Β»―ϋ÷±Ϋ«»ΐΫ«–Έ ±Θ§«σ≥ωΥυ”–ΖϊΚœΧθΦΰΒΡΒψ![]() ΒΡΉχ±ξΘΜ
ΒΡΉχ±ξΘΜ
ΔΎ»Γ![]() ΒΡ÷–Βψ
ΒΡ÷–Βψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§
Θ§![]() Θ§«σ
Θ§«σ![]() ΒΡΉν¥σ÷ΒΘ°
ΒΡΉν¥σ÷ΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©ΔΌ
ΘΜΘ®2Θ©ΔΌ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ΘΜΔΎ
ΘΜΔΎ![]() ΒΡΉν¥σ÷ΒΈΣ
ΒΡΉν¥σ÷ΒΈΣ![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©œ»«σ≥ωΒψ![]() ΒΡΉχ±ξΘ§»ΜΚσάϊ”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ω≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΘΜ
ΒΡΉχ±ξΘ§»ΜΚσάϊ”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ω≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®2Θ©ΔΌ Ήœ»«σ≥ω÷±œΏ![]() ΒΡΫβΈω ΫΚΆœΏΕΈ
ΒΡΫβΈω ΫΚΆœΏΕΈ![]() ΒΡ≥ΛΕ»Θ§ΉςΈΣΚσ–χΦΤΥψΒΡΜυ¥ΓΘ°
ΒΡ≥ΛΕ»Θ§ΉςΈΣΚσ–χΦΤΥψΒΡΜυ¥ΓΘ°
»τ![]() ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρΩ…Ζ÷ΈΣ“‘œ¬ΝΫ÷÷«ιΩωΘΚ
ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρΩ…Ζ÷ΈΣ“‘œ¬ΝΫ÷÷«ιΩωΘΚ
Β±![]() ΈΣ÷±Ϋ«±Ώ ±ΘΚΒψ
ΈΣ÷±Ϋ«±Ώ ±ΘΚΒψ![]() ΒΫ
ΒΫ![]() ΒΡΨύάκΈΣ
ΒΡΨύάκΈΣ![]() Θ°¥Υ ±Θ§ΫΪ÷±œΏ
Θ°¥Υ ±Θ§ΫΪ÷±œΏ![]() œρ”“ΤΫ“Τ4ΗωΒΞΈΜΚσΥυΒΟ÷±œΏ
œρ”“ΤΫ“Τ4ΗωΒΞΈΜΚσΥυΒΟ÷±œΏ![]() ”κ≈ΉΈοœΏΒΡΫΜΒψΘ§Φ¥ΈΣΥυ«σ÷°
”κ≈ΉΈοœΏΒΡΫΜΒψΘ§Φ¥ΈΣΥυ«σ÷°![]() ΒψΘΜ
ΒψΘΜ
Β±![]() ΈΣ–±±Ώ ±ΘΚΒψ
ΈΣ–±±Ώ ±ΘΚΒψ![]() ΒΫ
ΒΫ![]() ΒΡΨύάκΈΣ
ΒΡΨύάκΈΣ![]() Θ°¥Υ ±Θ§ΫΪ÷±œΏ
Θ°¥Υ ±Θ§ΫΪ÷±œΏ![]() œρ”“ΤΫ“Τ2ΗωΒΞΈΜΚσΥυΒΟ÷±œΏ
œρ”“ΤΫ“Τ2ΗωΒΞΈΜΚσΥυΒΟ÷±œΏ![]() ”κ≈ΉΈοœΏΒΡΫΜΒψΘ§Φ¥ΈΣΥυ«σ÷°
”κ≈ΉΈοœΏΒΡΫΜΒψΘ§Φ¥ΈΣΥυ«σ÷°![]() ΒψΘ°
ΒψΘ°
ΔΎ”…ΔΌΩ…÷ΣΘ§![]() ΈΣΕ®÷ΒΘ§“ρ¥ΥΒ±
ΈΣΕ®÷ΒΘ§“ρ¥ΥΒ±![]() »ΓΉν–Γ÷Β ±Θ§
»ΓΉν–Γ÷Β ±Θ§![]() ”–Ήν¥σ÷ΒΘ°
”–Ήν¥σ÷ΒΘ°
»γ¥πΆΦ2Υυ ΨΘ§ΉςΒψ![]() ΙΊ”Ύ÷±œΏ
ΙΊ”Ύ÷±œΏ![]() ΒΡΕ‘≥ΤΒψ
ΒΡΕ‘≥ΤΒψ![]() Θ§”…Ζ÷ΈωΩ…÷ΣΘ§Β±
Θ§”…Ζ÷ΈωΩ…÷ΣΘ§Β±![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ÷–ΒψΘ©»ΐΒψΙ≤œΏ ±Θ§
÷–ΒψΘ©»ΐΒψΙ≤œΏ ±Θ§![]() Ήν–ΓΘ§Ήν–Γ÷ΒΈΣœΏΕΈ
Ήν–ΓΘ§Ήν–Γ÷ΒΈΣœΏΕΈ![]() ΒΡ≥ΛΕ»Θ°
ΒΡ≥ΛΕ»Θ°
ΫβΘΚΘ®1Θ©![]() Β»―ϋ÷±Ϋ«»ΐΫ«–Έ
Β»―ϋ÷±Ϋ«»ΐΫ«–Έ![]() ΒΡΕΞΒψ
ΒΡΕΞΒψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§
Θ§![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]()
![]() Βψ
Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ°
Θ°
![]() ≈ΉΈοœΏΙΐ
≈ΉΈοœΏΙΐ![]() Θ§
Θ§![]() ΝΫΒψΘ§
ΝΫΒψΘ§
![]()
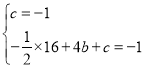 Θ§
Θ§
ΫβΒΟΘΚ![]() Θ§
Θ§![]() Θ§
Θ§
![]() ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΈΣΘΚ
≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΈΣΘΚ![]() Θ°
Θ°
Θ®2Θ©ΔΌ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
![]() ÷±œΏ
÷±œΏ![]() ΒΡΫβΈω ΫΈΣΘΚ
ΒΡΫβΈω ΫΈΣΘΚ![]() Θ°
Θ°
…ηΤΫ“Τ«Α≈ΉΈοœΏΒΡΕΞΒψΈΣ![]() Θ§‘ρ”…Θ®1Θ©Ω…ΒΟ
Θ§‘ρ”…Θ®1Θ©Ω…ΒΟ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§«“
Θ§«“![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ![]() …œΘ°
…œΘ°
![]() Βψ
Βψ![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ![]() …œΜ§Ε·Θ§
…œΜ§Ε·Θ§
![]() Ω……η
Ω……η![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§
Θ§
‘ρΤΫ“ΤΚσ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΈΣΘΚ![]() Θ°
Θ°
ΫβΖΫ≥ΧΉιΘΚ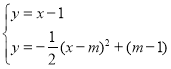 Θ§
Θ§
ΫβΒΟ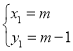 Θ§
Θ§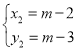
![]() Θ§
Θ§![]() Θ°
Θ°
ΙΐΒψ![]() Ής
Ής![]() ÷αΘ§ΙΐΒψ
÷αΘ§ΙΐΒψ![]() Ής
Ής![]() ÷αΘ§‘ρ
÷αΘ§‘ρ
![]() Θ§
Θ§![]() Θ°
Θ°
![]() Θ°
Θ°
»τ“‘![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() »ΐΒψΈΣΕΞΒψΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρΩ…Ζ÷ΈΣ“‘œ¬ΝΫ÷÷«ιΩωΘΚ
»ΐΒψΈΣΕΞΒψΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρΩ…Ζ÷ΈΣ“‘œ¬ΝΫ÷÷«ιΩωΘΚ
Β±![]() ΈΣ÷±Ϋ«±Ώ ±ΘΚΒψ
ΈΣ÷±Ϋ«±Ώ ±ΘΚΒψ![]() ΒΫ
ΒΫ![]() ΒΡΨύάκΈΣ
ΒΡΨύάκΈΣ![]() Θ®Φ¥ΈΣ
Θ®Φ¥ΈΣ![]() ΒΡ≥ΛΘ©Θ°
ΒΡ≥ΛΘ©Θ°
”…![]() Θ§
Θ§![]() Θ§
Θ§![]() Ω…÷ΣΘ§
Ω…÷ΣΘ§
![]() ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§«“
ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§«“![]() Θ§
Θ§![]() Θ°
Θ°
»γΆΦ1Θ§ΙΐΒψ![]() Ής÷±œΏ
Ής÷±œΏ![]() Θ§ΫΜ≈ΉΈοœΏ
Θ§ΫΜ≈ΉΈοœΏ![]() ”ΎΒψ
”ΎΒψ![]() Θ§‘ρ
Θ§‘ρ![]() ΈΣΖϊΚœΧθΦΰΒΡΒψΘ°
ΈΣΖϊΚœΧθΦΰΒΡΒψΘ°
![]() Ω……η÷±œΏ
Ω……η÷±œΏ![]() ΒΡΫβΈω ΫΈΣΘΚ
ΒΡΫβΈω ΫΈΣΘΚ![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
ΫβΒΟ![]() Θ§
Θ§
![]() ÷±œΏ
÷±œΏ![]() ΒΡΫβΈω ΫΈΣΘΚ
ΒΡΫβΈω ΫΈΣΘΚ![]() Θ°
Θ°
ΫβΖΫ≥ΧΉι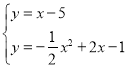 Θ§
Θ§
ΒΟΘΚ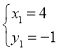 Θ§
Θ§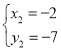
![]() Θ§
Θ§![]() Θ°
Θ°
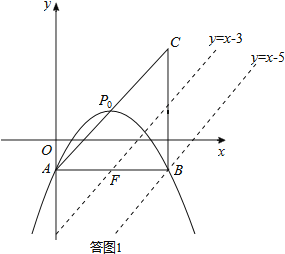
Β±![]() ΈΣ–±±Ώ ±ΘΚ
ΈΣ–±±Ώ ±ΘΚ![]() Θ§Ω…«σΒΟΒψ
Θ§Ω…«σΒΟΒψ![]() ΒΫ
ΒΫ![]() ΒΡΨύάκΈΣ
ΒΡΨύάκΈΣ![]() Θ°
Θ°
»γ¥πΆΦ2Θ§»Γ![]() ΒΡ÷–Βψ
ΒΡ÷–Βψ![]() Θ§‘ρΒψ
Θ§‘ρΒψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ°
Θ°
”…![]() Θ§
Θ§![]() Θ§
Θ§![]() Ω…÷ΣΘΚ
Ω…÷ΣΘΚ
![]() ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§«“Βψ
ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§«“Βψ![]() ΒΫ÷±œΏ
ΒΫ÷±œΏ![]() ΒΡΨύάκΈΣ
ΒΡΨύάκΈΣ![]() Θ°
Θ°
ΙΐΒψ![]() Ής÷±œΏ
Ής÷±œΏ![]() Θ§ΫΜ≈ΉΈοœΏ
Θ§ΫΜ≈ΉΈοœΏ![]() ”ΎΒψ
”ΎΒψ![]() Θ§‘ρ
Θ§‘ρ![]() ΈΣΖϊΚœΧθΦΰΒΡΒψΘ°
ΈΣΖϊΚœΧθΦΰΒΡΒψΘ°
![]() Ω……η÷±œΏ
Ω……η÷±œΏ![]() ΒΡΫβΈω ΫΈΣΘΚ
ΒΡΫβΈω ΫΈΣΘΚ![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
ΫβΒΟ![]() Θ§
Θ§
![]() ÷±œΏ
÷±œΏ![]() ΒΡΫβΈω ΫΈΣΘΚ
ΒΡΫβΈω ΫΈΣΘΚ![]() Θ°
Θ°
ΫβΖΫ≥ΧΉι Θ§
Θ§
ΒΟΘΚ Θ§
Θ§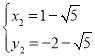
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ°
Θ°
Ήέ…œΥυ ωΘ§Υυ”–ΖϊΚœΧθΦΰΒΡΒψ![]() ΒΡΉχ±ξΈΣΘΚ
ΒΡΉχ±ξΈΣΘΚ
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ°
Θ°
ΔΎ![]() ¥φ‘ΎΉν¥σ÷ΒΘ°άμ”…»γœ¬ΘΚ
¥φ‘ΎΉν¥σ÷ΒΘ°άμ”…»γœ¬ΘΚ
”…ΔΌ÷Σ![]() ΈΣΕ®÷ΒΘ§‘ρΒ±
ΈΣΕ®÷ΒΘ§‘ρΒ±![]() »ΓΉν–Γ÷Β ±Θ§
»ΓΉν–Γ÷Β ±Θ§![]() ”–Ήν¥σ÷ΒΘ°
”–Ήν¥σ÷ΒΘ°
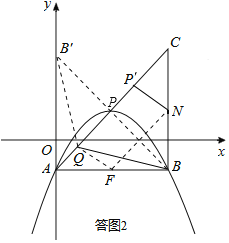
»γ¥πΆΦ2Θ§»ΓΒψ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΕ‘≥ΤΒψ
ΒΡΕ‘≥ΤΒψ![]() Θ§“ΉΒΟΒψ
Θ§“ΉΒΟΒψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§
Θ§![]() Θ°
Θ°
Ν§Ϋ”![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
“ΉΒΟ![]() Θ§«“
Θ§«“![]() Θ§
Θ§
![]() ΥΡ±Ώ–Έ
ΥΡ±Ώ–Έ![]() ΈΣΤΫ––ΥΡ±Ώ–ΈΘ°
ΈΣΤΫ––ΥΡ±Ώ–ΈΘ°
![]() Θ°
Θ°
![]() Θ°
Θ°
![]() Β±
Β±![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() »ΐΒψΙ≤œΏ ±Θ§
»ΐΒψΙ≤œΏ ±Θ§![]() Ήν–ΓΘ§Ήν–Γ÷ΒΈΣ
Ήν–ΓΘ§Ήν–Γ÷ΒΈΣ![]() Θ°
Θ°
![]()
![]() ΒΡΉν¥σ÷ΒΈΣ
ΒΡΉν¥σ÷ΒΈΣ![]() Θ°
Θ°

 ΩΣ–ΡΆήΉ¥‘Σ≤β ‘ΨμœΒΝ–¥πΑΗ
ΩΣ–ΡΆήΉ¥‘Σ≤β ‘ΨμœΒΝ–¥πΑΗΓΨΧβΡΩΓΩ»γΆΦ1Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() «÷Θ÷ί –ΕΰΤΏ«χ»ΐΗωά§Μχ¥φΖ≈ΒψΘ§Βψ
«÷Θ÷ί –ΕΰΤΏ«χ»ΐΗωά§Μχ¥φΖ≈ΒψΘ§Βψ![]() Θ§
Θ§![]() Ζ÷±πΈΜ”ΎΒψ
Ζ÷±πΈΜ”ΎΒψ![]() ΒΡ’ΐ±±ΚΆ’ΐΕΪΖΫœρΘ§
ΒΡ’ΐ±±ΚΆ’ΐΕΪΖΫœρΘ§![]() ΟΉΘ°ΑΥΈΜΜΖΈάΙΛ»ΥΖ÷±π≤βΒΟΒΡ
ΟΉΘ°ΑΥΈΜΜΖΈάΙΛ»ΥΖ÷±π≤βΒΟΒΡ![]() ≥ΛΕ»»γœ¬±μΘΚ
≥ΛΕ»»γœ¬±μΘΚ
ΦΉ | ΕΓ | ±ϊ | ΕΓ | Έλ | –γ | …ξ | ≥Ϋ | |
| 84 | 76 | 78 | 82 | 70 | 84 | 86 | 80 |
ΥϊΟ«”÷Βς≤ιΝΥΗςΒψΒΡά§ΜχΝΩΘ§≤ΔΜφ÷ΤΝΥœ¬Ν–Φδ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦ2Θ°
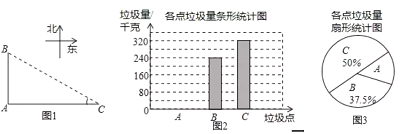
Θ®1Θ©±μ÷–ΒΡ÷–ΈΜ ΐ « ΓΔ÷Ύ ΐ « ΘΜ
Θ®2Θ©«σ±μ÷–![]() ≥ΛΕ»ΒΡΤΫΨυ ΐ
≥ΛΕ»ΒΡΤΫΨυ ΐ![]() ΘΜ
ΘΜ
Θ®3Θ©«σ![]() ¥ΠΒΡά§ΜχΝΩΘ§≤ΔΫΪΆΦ2≤Ι≥δΆξ’ϊΘΜ
¥ΠΒΡά§ΜχΝΩΘ§≤ΔΫΪΆΦ2≤Ι≥δΆξ’ϊΘΜ
Θ®4Θ©”ΟΘ®2Θ©÷–ΒΡ![]() ΉςΈΣ
ΉςΈΣ![]() ΒΡ≥ΛΕ»Θ§“ΣΫΪ
ΒΡ≥ΛΕ»Θ§“ΣΫΪ![]() ¥ΠΒΡά§Μχ―ΊΒά¬Ζ
¥ΠΒΡά§Μχ―ΊΒά¬Ζ![]() ΕΦ‘ΥΒΫ
ΕΦ‘ΥΒΫ![]() ¥ΠΘ§“―÷Σ‘ΥΥΆ1«ßΩΥά§ΜχΟΩΟΉΒΡΖ―”ΟΈΣ0.005‘ΣΘ§«σ‘Υά§ΜχΥυ–ηΒΡΖ―”ΟΘ°
¥ΠΘ§“―÷Σ‘ΥΥΆ1«ßΩΥά§ΜχΟΩΟΉΒΡΖ―”ΟΈΣ0.005‘ΣΘ§«σ‘Υά§ΜχΥυ–ηΒΡΖ―”ΟΘ°