题目内容
 如图,在平面直角坐标系中,点O位坐标原点,等边△OAB的点B的坐标为(6,0),点A在第一象限,点P从A出发沿线段AB以每秒2个单位的速度向B运动,同时点Q从O出发沿x轴也以每秒2个单位的速度向x轴负半轴运动,当点P停止时,点Q也随之停止,连接PQ,交边OA于点D.
如图,在平面直角坐标系中,点O位坐标原点,等边△OAB的点B的坐标为(6,0),点A在第一象限,点P从A出发沿线段AB以每秒2个单位的速度向B运动,同时点Q从O出发沿x轴也以每秒2个单位的速度向x轴负半轴运动,当点P停止时,点Q也随之停止,连接PQ,交边OA于点D.(1)设点P,Q运动时间为t秒(0<t<3),AD=m,试求m与t的关系式;
(2)t为何值时,∠OQP=30°;
(3)在(2)的条件下,点A关于PQ对称的点为E,连接DE,试判断DE与OB位置关系,并证明你的结论.
考点:全等三角形的判定与性质,坐标与图形性质,等边三角形的判定与性质
专题:动点型
分析:(1)过P作PC∥OB,交OA于点C,易证∠CPQ=∠OPQ,即可证明△DOQ≌△DCP,可得OD=CD,即可解题;
(2)易证OQ=OD,即可求得t的值,即可解题;
(3)在(2)的结论下可以证明∠APD=90°,即可得△ADP≌△EDP,即可求得∠ADE=60°=∠AOB,即可解题.
(2)易证OQ=OD,即可求得t的值,即可解题;
(3)在(2)的结论下可以证明∠APD=90°,即可得△ADP≌△EDP,即可求得∠ADE=60°=∠AOB,即可解题.
解答:解:(1)过P作PC∥OB,交OA于点C,如图1,
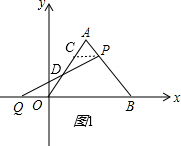
则△ACP为等边三角形,
∴AC=AP=CP=2t,
∵PC∥OB,
∴∠CPQ=∠OPQ,
在△DOQ和△DCP中,
,
∴△DOQ≌△DCP,(AAS)
∴OD=CD=
=3-t,
∴m=CD+AC=3-t+2t=3+t;
(2)∵∠AOB=∠OQD+∠ODQ=60°,
∠OQP=30°,
∴∠ODQ=30°,
∴OQ=OD,即2t=6-2t,
∴t=
,
∴t=
时,∠OQP=30°;
(3)过P作PC∥OB,交OA于点C,如图2,
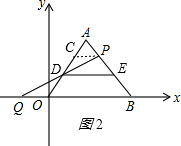
∵∠CPD=∠OQD=30°,∠APC=60°,
∴∠APD=90°,即AP⊥PD,
∴E点位于AE上,且△ADP≌△EDP,
∴∠ADE=∠ADP+∠PDE=2∠ADP=60°,
∵∠AOB=60°,
∴DE∥OB.

则△ACP为等边三角形,
∴AC=AP=CP=2t,
∵PC∥OB,
∴∠CPQ=∠OPQ,
在△DOQ和△DCP中,
|
∴△DOQ≌△DCP,(AAS)
∴OD=CD=
| 6-2t |
| 2 |
∴m=CD+AC=3-t+2t=3+t;
(2)∵∠AOB=∠OQD+∠ODQ=60°,
∠OQP=30°,
∴∠ODQ=30°,
∴OQ=OD,即2t=6-2t,
∴t=
| 3 |
| 2 |
∴t=
| 3 |
| 2 |
(3)过P作PC∥OB,交OA于点C,如图2,

∵∠CPD=∠OQD=30°,∠APC=60°,
∴∠APD=90°,即AP⊥PD,
∴E点位于AE上,且△ADP≌△EDP,
∴∠ADE=∠ADP+∠PDE=2∠ADP=60°,
∵∠AOB=60°,
∴DE∥OB.
点评:本题考查了全等三角形的判定和全等三角形对应边、对应角相等的性质,本题中求证△DOQ≌△DCP是解题的关键.

练习册系列答案
相关题目
 如图,若∠A+∠B+∠C+∠D=180°,AD与BC相交于点O,你能说明DE与CF平行吗?
如图,若∠A+∠B+∠C+∠D=180°,AD与BC相交于点O,你能说明DE与CF平行吗? 如图,三角形ABC的边BC:AB=3:1,请求出点A到BC的距离与点C到AB的距离的比.
如图,三角形ABC的边BC:AB=3:1,请求出点A到BC的距离与点C到AB的距离的比.