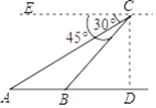
题目内容
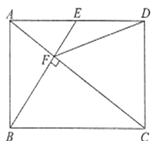
【题目】如图,![]() 中,
中,![]() 分别在四条边上.
分别在四条边上.![]() ,
,![]() ,
,![]() ,
,![]() .
.
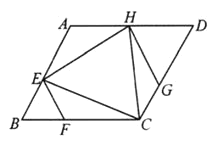
(1)写出图中的相似三角形,并证明.
(2)当![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)![]() ∽
∽![]() ,
,![]() ∽
∽![]() .证明见解析;(2)
.证明见解析;(2)![]()
【解析】
(1)先求出![]() 、
、![]() 是等边三角形.从而可证
是等边三角形.从而可证![]() ∽
∽![]() .根据两角分别相等的两个三角形相似,可证
.根据两角分别相等的两个三角形相似,可证![]() ∽
∽![]() .
.
(2)设![]() .则
.则![]() ,
,![]() .从而可得
.从而可得![]() ,
,![]() .利用相似三角形对应边成比例,可得
.利用相似三角形对应边成比例,可得![]() , 即得
, 即得![]() , 解出
, 解出![]() 值并检验即得. 作
值并检验即得. 作![]() 于
于![]() .则
.则![]() ,根据30°角所对的直角边等于斜边的一半,可得
,根据30°角所对的直角边等于斜边的一半,可得![]() ,从而求出
,从而求出![]() ,继而求出
,继而求出![]() 的长.
的长.
(1)解:![]() ∽
∽![]() ,
,![]() ∽
∽![]() .证明如下:
.证明如下:
∵![]() 是平行四边形,∴
是平行四边形,∴![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() 是等边三角形.
是等边三角形.
同理,![]() 是等边三角形.
是等边三角形.
∴![]() ∽
∽![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ∽
∽![]() .
.
(2)解:设![]() .则
.则![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
由![]() ∽
∽![]() ,得
,得![]()
∴![]()
∴![]() .
.
∴![]() .取正根
.取正根![]()
作![]() 于
于![]() .则
.则![]()
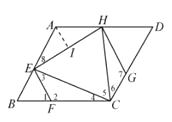
∵![]() , ∴
, ∴![]() ∴
∴![]() ∴
∴![]() .
.
∴![]() .
.
故答案为:(1)![]() ∽
∽![]() ,
,![]() ∽
∽![]() .证明见解析;(2)
.证明见解析;(2)![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目