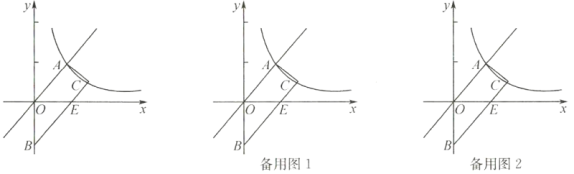
题目内容
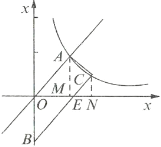
【题目】如图所示,梯形![]() 的顶点
的顶点![]() 、
、![]() 在反比例函数
在反比例函数![]() 图像上,
图像上,![]() ,上底边
,上底边![]() 在直线
在直线![]() 上,下底边
上,下底边![]() 交
交![]() 轴于
轴于![]() ,点
,点![]() 的纵坐标是1.
的纵坐标是1.
(1)求反比例函数的解析式;
(2)求四边形![]() 的面积;
的面积;
(3)若将点![]() 的坐标改为
的坐标改为![]() ,且
,且![]() ,其他条件不变,探究四边形
,其他条件不变,探究四边形![]() 的面积;
的面积;
(4)若将点![]() 的坐标改为
的坐标改为![]() ,且
,且![]() ,点
,点![]() 的纵坐标改为
的纵坐标改为![]() ,且
,且![]() ,其他条件不变,直接写出四边形
,其他条件不变,直接写出四边形![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)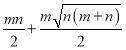
【解析】
(1)如图所示,过点![]() ,
,![]() 分别作
分别作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,![]() ,由于上底边在直线y=x上,故可得出
,由于上底边在直线y=x上,故可得出![]() ,
,![]() ,然后结合题意可求得点C坐标,进而可得结果;
,然后结合题意可求得点C坐标,进而可得结果;
(2)先联立![]() 与
与![]() 组成方程组,解方程组即得点A坐标,即为AM和OM的长,然后利用S四边形AOEC=S△AOM+S梯形AMNC-S△CEN代入相关数据求解即可;
组成方程组,解方程组即得点A坐标,即为AM和OM的长,然后利用S四边形AOEC=S△AOM+S梯形AMNC-S△CEN代入相关数据求解即可;
(3)根据题意可求得点C坐标,进而可得反比例函数关系式,然后仿(2)的思路求出点A坐标,再利用S四边形AOEC=S△AOM+S梯形AMNC-S△CEN代入相关数据求解即可;
(4)根据题意可求得点C坐标,进而可得反比例函数关系式,然后仿(3)的思路求出点A坐标,再利用S四边形AOEC=S△AOM+S梯形AMNC-S△CEN代入相关数据求解即可.
(1)如图所示,过点![]() ,
,![]() 分别作
分别作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,![]() ,
,
∵OA在直线y=x上,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵点![]() 的纵坐标为1,∴
的纵坐标为1,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,即
,即![]() ;
;
(2)将![]() 与
与![]() 组成方程组得
组成方程组得![]() ,解得
,解得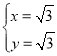 ,或
,或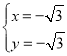 (舍去),
(舍去),
∴AM=OM=![]() ,将
,将![]() 代入
代入![]() 得:
得:![]() ,即
,即![]() 点的横坐标为3,
点的横坐标为3,
∴![]() ,
,
∴S四边形AOEC=S△AOM+S梯形AMNC-S△CEN![]() .
.
(3)∵点![]() 的纵坐标为1,点
的纵坐标为1,点![]() ,∴点
,∴点![]() .
.
∵点![]() 在反比例函数的图像上,∴
在反比例函数的图像上,∴![]() ,
,
解方程组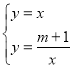 ,得
,得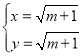 ,或
,或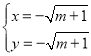 (舍去),
(舍去),
∴点![]() 的坐标为
的坐标为![]() .
.
∴S四边形AOEC=S△AOM+S梯形AMNC-S△CEN ![]()
![]() ;
;

(4)∵点![]() 的纵坐标为n,点
的纵坐标为n,点![]() ,∴点
,∴点![]() .
.
∵点![]() 在反比例函数的图像上,∴
在反比例函数的图像上,∴![]() ,
,
解方程组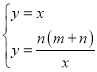 ,得
,得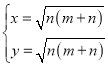 ,或
,或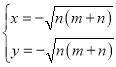 (舍去),
(舍去),
∴S四边形AOEC=S△AOM+S梯形AMNC-S△CEN![]()
![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某弹簧挂上不超过20千克的物体后按一定规律伸长,测得一弹簧的长度![]() (厘米)与所挂的物体的质量
(厘米)与所挂的物体的质量![]() (千克)有下面的关系:
(千克)有下面的关系:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 | 16 |
那么弹簧的总长![]() (厘米)与所挂的物体的质量
(厘米)与所挂的物体的质量![]() (千克)之间是否是函数关系?若是,请写出函数关系式.
(千克)之间是否是函数关系?若是,请写出函数关系式.