题目内容
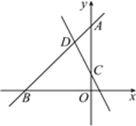
【题目】如图,直线y=kx+4(k≠0)与x轴、y轴分别交于点B,A,直线y=-2x+1与y轴交于点C,与直线y=kx+4交于点D,△ACD的面积是![]() .
.
(1)求直线AB的表达式;
(2)设点E在直线AB上,当△ACE是直角三角形时,求出点E的坐标.
【答案】(1)y=x+4;(2)点E的坐标为(![]() 3,1)或(
3,1)或(![]()
![]() ,
,![]() ).
).
【解析】
(1)将x=0分别代入两个一次函数表达式中求出点A、C的坐标,进而即可得出AC的长度,再根据三角形的面积公式结合△ACD的面积即可求出点D的横坐标,利用一次函数图象上点的坐标特即可求出点D的坐标,由点D的坐标利用待定系数法即可求出直线AB的表达式;
(2)由直线AB的表达式即可得出△ACE为等腰直角三角形,分∠ACE=90°和∠AEC=90°两种情况考虑,根据点A、C的坐标利用等腰直角三角形的性质即可得出点E的坐标,此题得解.
解:(1)当x=0时,y=kx+4=4,y=-2x+1=1,
∴A(0,4),C(0,1),
∴AC=3.
∵S△ACD=![]() ,
,
∴![]() ,
,
∵点D在第二象限,
点D的横坐标为![]() .
.
当x=![]() 时,y=
时,y=![]() 2x+1=3,
2x+1=3,
∴D(![]() 1,3).
1,3).
将D(![]() 1,3)代入y=kx+4,
1,3)代入y=kx+4,
![]() k+4=3,解得:k=1.
k+4=3,解得:k=1.
∴直线AB的表达式为:y=x+4.
(2)∵直线AB的表达式为y=x+4,
∴△ACE为等腰直角三角形.
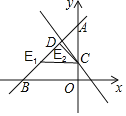
当∠ACE=90°时,∵A(0,4),C(0,1),AC=3,
∴E1(![]() 3,1);
3,1);
当∠AEC=90°时,∵A(0,4),C(0,1),AC=3,
∴E2(![]()
![]() ,
,![]() ).
).
综上所述:当△ACE是直角三角形时,点E的坐标为(![]() 3,1)或(
3,1)或(![]()
![]() ,
,![]() ).
).

 一线名师提优试卷系列答案
一线名师提优试卷系列答案【题目】某弹簧挂上不超过20千克的物体后按一定规律伸长,测得一弹簧的长度![]() (厘米)与所挂的物体的质量
(厘米)与所挂的物体的质量![]() (千克)有下面的关系:
(千克)有下面的关系:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 | 16 |
那么弹簧的总长![]() (厘米)与所挂的物体的质量
(厘米)与所挂的物体的质量![]() (千克)之间是否是函数关系?若是,请写出函数关系式.
(千克)之间是否是函数关系?若是,请写出函数关系式.