Question

5．已知AD和CE是△ABC的高，且S_△BDE：S_△ABC=1；4，若AD=4$\sqrt{3}$，则AB=8．

Answer 1

分析 先根据∠ADB=∠CEB，∠B=∠B，得出△ABD∽△CBE，再根据相似三角形的对应边成比例，列出比例式$\frac{BD}{BA}$=$\frac{BE}{BC}$，再结合∠B=∠B，判定△BDE∽△BAC，最后根据相似三角形的性质，以及勾股定理，求得AB的长．

解答 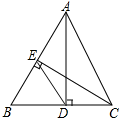解：∵AD和CE是△ABC的高，
∴∠ADB=∠CEB，
又∵∠B=∠B，
∴△ABD∽△CBE，
$\frac{BD}{BE}$=$\frac{BA}{BC}$，即$\frac{BD}{BA}$=$\frac{BE}{BC}$，
又∵∠B=∠B，
∴△BDE∽△BAC，
∴$\frac{{S}_{△BDE}}{{S}_{△ABC}}$=$（\frac{DE}{AC}）^{2}$=$\frac{1}{4}$，
∴$\frac{DE}{AC}$=$\frac{1}{2}$=$\frac{BD}{BA}$，
设BD=x，则AB=2x，
Rt△ABD中，BD²+AD²=AB²，
即${x}^{2}+（4\sqrt{3}）^{2}=（2x）^{2}$，
解得x=4，
∴AB=8．

点评 本题主要考查了三角形的面积计算，解决问题的关键是掌握相似三角形的判定与性质，解题时注意：相似三角形的面积之比等于相似比的平方．