题目内容
11．
某学校组织团员举行申奥成功宣传活动，从学校骑车出发，先上坡到达A地后，宣传8分钟；然后下坡到B地宣传8分钟返回，行程情况如图．若返回时，上、下坡速度仍保持不变，在A地仍要宣传8分钟，那么他们从B地返回学校用的时间是（ ）| A． | 45.2分钟 | B． | 48分钟 | C． | 46分钟 | D． | 33分钟 |
分析 由图象可知校车在上坡时的速度为200米每分钟，长度为3600米；下坡时的速度为500米每分钟，长度为6000米；又因为返回时上下坡速度不变，总路程相等，根据题意列出各段所用时间相加即可得出答案．
解答 解：由上图可知，上坡的路程为3600米，速度为200米每分钟；
下坡时的路程为6000米，速度为6000÷（46-18-8×2）=500米每分钟；
由于返回时上下坡互换，变为上坡路程为6000米，所以所用时间为30分钟；
停8分钟；
下坡路程为3600米，所用时间是7.2分钟；
故总时间为30+8+7.2=45.2分钟．
故选A．
点评 本题考查利用函数的图象解决实际问题，学生对分段问题的处理能力和往返问题的理解是解题的关键．
练习册系列答案
相关题目
4．
如图中阴影部分面积的是（ ）
如图中阴影部分面积的是（ ）| A． | 2x+5 | B． | x2+3x+5 | C． | x2+5x+6 | D． | x2+3x+6 |
19．在-3、0、π、$\sqrt{3}$这四个数中，最大的有理数是（ ）
| A． | 0 | B． | -3 | C． | π | D． | $\sqrt{3}$ |
6．下列算式能用平方差公式计算的是（ ）
| A． | （2a+b）（2b-a） | B． | （a+1）（-a-1） | C． | （3x-y）（-3x+y） | D． | （-m-n）（-m+n） |
如图，点E在CD延长线上，下列条件①∠1=∠2，②∠3=∠4，③∠5=∠B，④∠B+∠BDC=180°，不能判定AB∥CD的有（ ）
1．
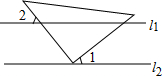如图，直线l1∥l2，直角三角形ABC的直角顶点C在直线l2上，若∠1=30°，则∠2的度数为（ ）
如图，直线l1∥l2，直角三角形ABC的直角顶点C在直线l2上，若∠1=30°，则∠2的度数为（ ）| A． | 30° | B． | 40° | C． | 50° | D． | 60° |
18．
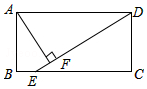如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（ ）
如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（ ）| A． | △AFD≌△DCE | B． | 2AF=AD | C． | AB=AF | D． | BE=AD-DF |
18．
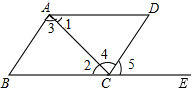如图，点E在BC的延长线上，下列条件中能判断AB∥CD的是（ ）
如图，点E在BC的延长线上，下列条件中能判断AB∥CD的是（ ）| A． | ∠1=∠2 | B． | ∠3=∠4 | C． | ∠D+∠BCD=180° | D． | ∠D=∠5 |