题目内容
 在平面直角坐标系xOy中,抛物线y=-x2+bx+c经过点(-3,0)和(1,0).
在平面直角坐标系xOy中,抛物线y=-x2+bx+c经过点(-3,0)和(1,0).(1)求抛物线的表达式;
(2)在给定的坐标系中,画出此抛物线;
(3)设抛物线顶点关于y轴的对称点为A,记抛物线在第二象限之间的部分为图象G.点B是抛物线对称轴上一动点,如果直线AB与图象G有公共点,请结合函数的图象,直接写出点B纵坐标t的取值范围.
考点:待定系数法求二次函数解析式,二次函数的图象,二次函数的性质
专题:
分析:(1)根据待定系数法即可求得;
(2)正确画出图形;
(3)通过图象可以看出点B纵坐标t的取值范围.
(2)正确画出图形;
(3)通过图象可以看出点B纵坐标t的取值范围.
解答:解:(1)∵抛物线y=-x2+bx+c经过点(-3,0)和(1,0).
∴
,
解得
,
∴抛物线的表达式为y=-x2-2x+3.
(2)此抛物线如图所示.

(3)2<t≤4.
如图,

由图象可知点B纵坐标t的取值范围为2<t≤4.
∴
|
解得
|
∴抛物线的表达式为y=-x2-2x+3.
(2)此抛物线如图所示.

(3)2<t≤4.
如图,

由图象可知点B纵坐标t的取值范围为2<t≤4.
点评:本题考查了待定系数法求解析式,以及画图的能力和识别图形的能力,要熟练掌握.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
将抛物线y=2x2向右平移1个单位,再向上平移3个单位,得到的抛物线是( )
| A、y=2(x+1)2+3 |
| B、y=2(x-1)2+3 |
| C、y=2(x+1)2-3 |
| D、y=2(x-1)2-3 |
若a=-1,则代数式2a2-3a+1的值是( )
| A、2 | B、0 | C、6 | D、-4 |
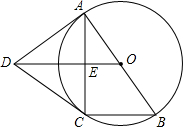 如图,AB是⊙O直径,AC是弦,OE⊥AC于点E,过A作⊙O的切线DA,DA与OE的延长线交于点D,连接DC,BC.
如图,AB是⊙O直径,AC是弦,OE⊥AC于点E,过A作⊙O的切线DA,DA与OE的延长线交于点D,连接DC,BC.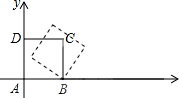 如图,边长为1的正方形ABCD 放置在平面直角坐标系中,顶点A与坐标原点O 重合,点B在x轴上.将正方形ABCD沿x轴正方向作无滑动滚动,当点D第一次落在x轴上时,D点的坐标是
如图,边长为1的正方形ABCD 放置在平面直角坐标系中,顶点A与坐标原点O 重合,点B在x轴上.将正方形ABCD沿x轴正方向作无滑动滚动,当点D第一次落在x轴上时,D点的坐标是