题目内容
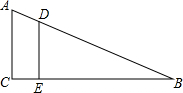填写理由：如图所示，因为∠A=∠BDE（已知），
所以
AC
AC
∥DE
DE
（同位角相等，两直线平行
同位角相等，两直线平行
）所以∠DEB=
∠C
∠C
（两直线平行，同位角相等
两直线平行，同位角相等
）因为∠C=90°（已知），
所以∠DEB=
90
90
°（等量代换
等量代换
）所以DE⊥
BC
BC
（垂直定义
垂直定义
）分析：当∠A=∠BDE根据同位角相等两直线平行可得AC∥DE，根据两直线平行，同位角相等可得∠DEB=∠C，根据∠C=90°可得∠DEB=90°，再根据垂直定义可得DE⊥BC．
解答：解：因为∠A=∠BDE（已知），
所以 AC∥DE（ 同位角相等，两直线平行），
所以∠DEB=∠C（ 两直线平行，同位角相等），
因为∠C=90°（已知），
所以∠DEB=90°（ 等量代换），
所以DE⊥BC（ 垂直定义）．
所以 AC∥DE（ 同位角相等，两直线平行），
所以∠DEB=∠C（ 两直线平行，同位角相等），
因为∠C=90°（已知），
所以∠DEB=90°（ 等量代换），
所以DE⊥BC（ 垂直定义）．
点评：此题主要考查了平行线的判定与性质，关键是掌握同位角相等两直线平行，两直线平行，同位角相等．
练习册系列答案
名校课堂系列答案
相关题目
填写理由：如图所示，
填写理由：
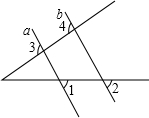填写理由：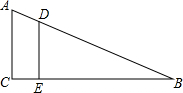
填写理由：如图所示，