题目内容
如图,∠1=∠2,则下列结论一定成立的是( )
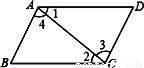
A. AB∥CD B. AD∥BC C. ∠B=∠D D. ∠3=∠4
练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
若分式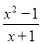 有意义,则x的取值范围为_________.
有意义,则x的取值范围为_________.
 x≠-1
【解析】由题意得
x+1≠0,
∴x≠-1.
x≠-1
【解析】由题意得
x+1≠0,
∴x≠-1. 题目内容
如图,∠1=∠2,则下列结论一定成立的是( )

A. AB∥CD B. AD∥BC C. ∠B=∠D D. ∠3=∠4
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案若分式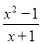 有意义,则x的取值范围为_________.
有意义,则x的取值范围为_________.
 x≠-1
【解析】由题意得
x+1≠0,
∴x≠-1.
x≠-1
【解析】由题意得
x+1≠0,
∴x≠-1.