题目内容
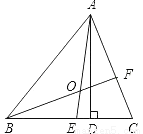
如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=54°,∠C=66°,求∠DAC、∠BOA的度数.
【答案】∠DAC=24°,∠BOA=123°
【解析】试题分析:因为AD是高,所以∠ADC=90°,又因为∠C=66°,所以∠DAC度数可求;因为∠BAC=54°,∠C=66°,所以∠BAO=27°,∠ABC=60°,BF是∠ABC的角平分线,则∠ABO=30°,故∠BOA的度数可求.
试题解析:∵AD是高,∴∠ADC=90° ,
∵∠C=66°,
∴∠DAC=180°﹣90°﹣66°=24°
∵∠BAC=54°,∠C=66°,AE是角平分线,
∴∠BAO=27°,∠ABC=60°
∵BF是∠ABC的角平分线 ,
∴∠ABO=30°,
∴∠BOA=180°﹣∠BAO﹣∠ABO=123°.
考点:1.三角形的外角性质;2.角平分线的定义;3.三角形内角和定理.
【题型】解答题
【结束】
23
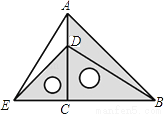
把两个含有45°角的直角三角板如图放置,点D在AC上,连接AE、BD,试判断AE与BD的关系,并说明理由.
练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目


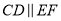 ,
, 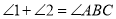 ,求证:
,求证: 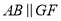 .
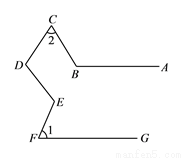
.
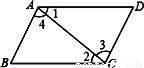
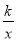 (k≠0)的图象上,则该函数的解析式为( )
(k≠0)的图象上,则该函数的解析式为( )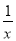 B. y=
B. y=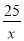 C. y=-
C. y=-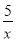 D. y=5x
D. y=5x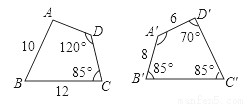
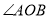 的平分线方法如下:以
的平分线方法如下:以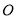 为圆心,任意长为半径画弧交
为圆心,任意长为半径画弧交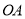 、
、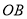 于
于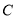 、
、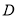 ,再分别以点
,再分别以点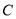 、
、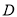 为圆心,以大于
为圆心,以大于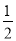 CD长为半径画弧,两弧交于点
CD长为半径画弧,两弧交于点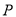 ,作射线
,作射线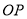 ,由作法得△OCP≌△ODP的根据是( )
,由作法得△OCP≌△ODP的根据是( )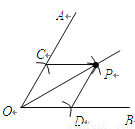
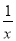 ) ⑥3xn+2+27xn=3xn(x2+9)
) ⑥3xn+2+27xn=3xn(x2+9)