题目内容
如图,n+1个边长为2的等边三角形有一条边在同一直线上,设△E1B2D2的面积为S1,△E2B3D3的面积为S2,…,△EnBn+1Dn+1的面积为Sn,则S1=________,Sn=________.



分析:根据等边三角形的性质求出等边三角形的高,连接B1Bn+1,可得B1Bn+1为n个边长为2的等边三角形的一边所在的直线,然后根据相似三角形对应边成比例求出
 ,B2D2,再根据等边三角形的性质求出点E1到B2D2的距离,然后利用三角形的面积公式求出S1,依此类推求出EnBn+1、Bn+1Dn+1,再求出点En到Bn+1Dn+1的距离,然后根据三角形的面积公式列式计算即可得解.
,B2D2,再根据等边三角形的性质求出点E1到B2D2的距离,然后利用三角形的面积公式求出S1,依此类推求出EnBn+1、Bn+1Dn+1,再求出点En到Bn+1Dn+1的距离,然后根据三角形的面积公式列式计算即可得解.解答:
 解:∵等边三角形的边长为2,
解:∵等边三角形的边长为2,∴等边三角形的高为2×
 =
= ,
,如图,连接B1Bn+1,则B1Bn+1为n个边长为2的等边三角形的一边所在的直线,
∴B1Bn+1∥ACn,
∴△AC1E1∽△B3B2E1,△AC2D2∽△B3B2D2,
∴
 =
= =
= =1,
=1, =
= =
= =
= ,
,∴
 =
=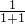 =
= ,B2D2=2×
,B2D2=2× =
= ,
,∴点E1到B2D2的距离=
 ×
× =
= ,
,∴S1=
 B2D2•
B2D2• =
= •
• •
• =
= ;
;同理可求,点E2到B3D3的距离=
 ×
× =
= ,
,…,
点En到Bn+1Dn+1的距离=
 ×
× =
= ,
,B3D3=2×
 =
= ,
,…,
Bn+1Dn+1=2×
 =
= ,
,∴Sn=
 •
• •
• =
= .
.故答案为:
 ;
; .
.点评:本题考查了相似三角形的判定与性质,等边三角形的判定与性质,作辅助线得到平行线从而得到相似三角形是解题的关键.

练习册系列答案
相关题目
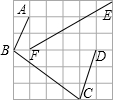 如图是由36个边长为1的小正方形拼成的,连接小正方形中的点A、B、C、D、E、F得线段AB、BC、CD、EF,这些线段中长度是有理数的是哪些?长度是无理数的是哪些?说明理由.
如图是由36个边长为1的小正方形拼成的,连接小正方形中的点A、B、C、D、E、F得线段AB、BC、CD、EF,这些线段中长度是有理数的是哪些?长度是无理数的是哪些?说明理由.

 已知△ABC,AB=3,BC=
已知△ABC,AB=3,BC=