题目内容
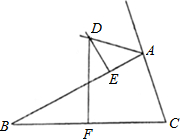如图，△ABC的边BC的中垂线DF交△BAC的外角平分线AD于D，F为垂足，DE⊥AB于E，且AB＞AC，求证：BE-AC=AE．
分析：作DG⊥AC，连接BD、CD，易证△ADE≌△ADG，得AE=AG，只要再证明△BED≌△CGD，即可得到；
解答：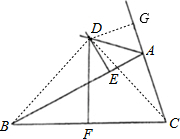
证明：作DG⊥AC，连接BD、CD，
∵AD是外角∠BAG的平分线，DE⊥AB，
∴∠DAE=∠DAG，
则在△ADE与△ADG中，
∴△ADE≌△ADG（AAS），
∴AE=AG，
∵DF是BC的中垂线，
∴BD=CD，
∴在Rt△BED和Rt△CGD中，
，
∴Rt△BED≌Rt△CGD（HL），
∴BE=CG=AC+AG，AG=AE，
∴BE-AC=AE．
证明：作DG⊥AC，连接BD、CD，∵AD是外角∠BAG的平分线，DE⊥AB，
∴∠DAE=∠DAG，
则在△ADE与△ADG中，
|
∴△ADE≌△ADG（AAS），
∴AE=AG，
∵DF是BC的中垂线，
∴BD=CD，
∴在Rt△BED和Rt△CGD中，
|
∴Rt△BED≌Rt△CGD（HL），
∴BE=CG=AC+AG，AG=AE，
∴BE-AC=AE．
点评：本题主要考查了全等三角形的判定与性质、线段垂直平分线的性质和角平分线的性质，考查了学生综合运用知识解决问题的能力，作辅助线构建全等三角形，是解答本题的关键．
练习册系列答案
相关题目
25、如图，△ABC的边AB、AC上分别有定点M、N，请在BC边上找一点P，使得△PMN的周长最短． （写出作法，保留作图痕迹）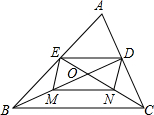
如图，△ABC的边AC、AB上的中线BD、CE相交于点O，M、N分别是BO、CO的中点，顺次连接点D、E、M、N．
如图，△ABC的边BC的垂直平分线MN交AC于D，若AC=6cm，AB=4cm，则△ADB的周长=
如图：△ABC的边AB的垂直平分线分别交BC、AB于M、N，△ACM的周长为10cm，AN=4cm．则△ABC的周长是（ ）cm．
如图，△ABC的边BC上的高为AD，且BC=9cm，AD=2cm，AB=6cm．