题目内容
4.解下列各题:(1)解方程组$\left\{\begin{array}{l}2(x+1)-y=6\\ \frac{x}{3}=y-1\end{array}\right.$
(2)化简:$\sqrt{12}$+$\sqrt{27}$+$\frac{1}{4}$$\sqrt{48}$-15$\sqrt{\frac{1}{3}}$
(3)解不等式:$\frac{{2{x^\_}1}}{3}$≤$\frac{x}{2}$,并把它的解集表示在数轴上
(4)解不等式组:$\left\{\begin{array}{l}2x-1>x\\ 3-2x≥x+3\end{array}\right.$,并把它的解集表示在数轴上.
分析 (1)先把方程组中的方程化为不含分母及括号的方程,再用加减消元法或代入消元法求解即可;
(2)先把各二次根式化为最减二次根式,再合并同类项即可;
(3)先去分母,再去括号,移项,合并同类项,把x的系数化为1,并在数轴上表示出来即可;
(4)分别求出各不等式的解集,再在数轴上表示出来即可.
解答 解:(1)原方程可化为$\left\{\begin{array}{l}2x-y=4①\\ x-3y=-3②\end{array}\right.$,
①-②×2得,5y=10,解得y=2,把y=2代入①得,2x-2=4,解得x=3,
故方程组的解集为:$\left\{\begin{array}{l}x=3\\ y=2\end{array}\right.$;
(2)原式=2$\sqrt{3}$+3$\sqrt{3}$+$\sqrt{3}$-5$\sqrt{3}$
=$\sqrt{3}$;
(3)去分母得,2(2x-1)≤3x,
去括号得,4x-2≤3x,
移项得,4x-3x≤2,
合并同类项得,x≤2.
在数轴上表示为: ;
;
(4)$\left\{\begin{array}{l}2x-1>x①\\ 3-2x≥x+3②\end{array}\right.$,
由①得,x>1,
由②得,x≤0,
故不等式组的解集为空集.
在数轴上表示为: .
.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
16.在公式S=$\frac{1}{2}$(a+b)h中,已知a=3,b=4,h=-4,那么S=( )
| A. | -14 | B. | 14 | C. | 28 | D. | -28 |
13.某超市一月份的营业额为200万元,三月份的营业额为288万元,如果每月比上一个月增长的百分数相同,则每月的平均增长率为( )
| A. | 10% | B. | 15% | C. | 20% | D. | 25% |
 在平面直角系中,已知A(-2,0),B(0,4),C(3,6);
在平面直角系中,已知A(-2,0),B(0,4),C(3,6);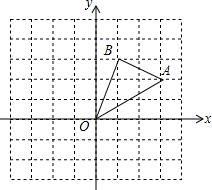 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,2),B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,2),B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1. 画出如图的主视图、左视图和俯视图.
画出如图的主视图、左视图和俯视图.