题目内容
5.观察下列各式:12-02=1+0=1;22-12=2+1=3;32-22=3+2=5;42-32=4+3=7;…若用字母n表示自然数.(1)请你把观察出的规律用含n的式子表示出来;
(2)你的猜想正确吗?试用有关的知识加以说明;
(3)求(2+1)(22+1)(24+1)(28+1)(216+1)的值.
分析 (1)观察给定的等式,根据等式的变化找出规律“(n+1)2-n2=2n+1”;
(2)利用完全平方公式的展开式结合整式的加减运算法则,来证明寻找到的规律成立;
(3)将算式×(2-1),算式的结果不变,结合平方差公式即可得出结论.
解答 解:(1)观察,发现规律:12-02=1,22-12=3,32-22=5,42-32=7,…,
则(n+1)2-n2=2n+1.
(2)证明:左边=(n+1)2-n2=n2+2n+1-n2=2n+1=右边,
故(1)的结论正确.
(3)(2+1)(22+1)(24+1)(28+1)(216+1)
=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)
=232-1
=1023.
点评 本题考查了规律型中的数字的变化类、完全平方公式以及平方差公式,解题的关键:(1)找出规律“(n+1)2-n2=2n+1”;(2)熟练的利用完全平方公式来证明结论;(3)将算式×(2-1).本题属于基础题,难度不大,解决该题型题目时,根据等式的变化找出变化规律是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.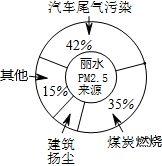 如图,是丽水PM2.5来源统计图,则根据统计图得出的下列判断中,正确的是( )
如图,是丽水PM2.5来源统计图,则根据统计图得出的下列判断中,正确的是( )
 如图,是丽水PM2.5来源统计图,则根据统计图得出的下列判断中,正确的是( )
如图,是丽水PM2.5来源统计图,则根据统计图得出的下列判断中,正确的是( )| A. | 汽车尾气约为建筑扬尘的3倍 | B. | 表示建筑扬尘的占7% | ||
| C. | 表示煤炭燃烧的圆心角约126° | D. | 煤炭燃烧的影响最大 |
9.在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:
①f(a,b)=(-a,b).如:f(1,3)=(-1,3);
②g(a,b)=(b,a).如:g(1,3)=(3,1);
③h(a,b)=(-a,-b).如,h(1,3)=(-1,-3).
按照以上变换有:f(g(h(2,-3)))=f(g(-2,3))=f(3,-2)=(-3,-2),
那么f(g(h(-3,5)))等于( )
①f(a,b)=(-a,b).如:f(1,3)=(-1,3);
②g(a,b)=(b,a).如:g(1,3)=(3,1);
③h(a,b)=(-a,-b).如,h(1,3)=(-1,-3).
按照以上变换有:f(g(h(2,-3)))=f(g(-2,3))=f(3,-2)=(-3,-2),
那么f(g(h(-3,5)))等于( )
| A. | (-5,-3) | B. | (5,3) | C. | (5,-3) | D. | (-5,3) |
15. 下列各展开图中,不能折成如图长方体的是( )
下列各展开图中,不能折成如图长方体的是( )
 下列各展开图中,不能折成如图长方体的是( )
下列各展开图中,不能折成如图长方体的是( )| A. |  | B. |  | C. |  | D. |  |
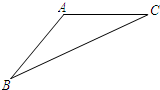 如图,△ABC中,AB=AC.
如图,△ABC中,AB=AC.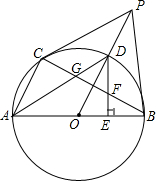 如图,AB为直径,PB为切线,点C在⊙O上,AC∥OP,连接OP,交⊙O点D,交BC于点H,过D点作DE⊥AB,E为垂足,交BC于点F,连AD交BC于G
如图,AB为直径,PB为切线,点C在⊙O上,AC∥OP,连接OP,交⊙O点D,交BC于点H,过D点作DE⊥AB,E为垂足,交BC于点F,连AD交BC于G