题目内容
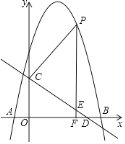
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是抛物线上一动点,过点
是抛物线上一动点,过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若点
若点![]() 在
在![]() 轴上方的抛物线上,当
轴上方的抛物线上,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
![]() 若点
若点![]() ’是点
’是点![]() 关于直线
关于直线![]() 的对称点,当点
的对称点,当点![]() ’落在
’落在![]() 轴上时,请直接写出
轴上时,请直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 的坐标为
的坐标为![]() 或
或![]() ;(3)m的值为
;(3)m的值为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用待定系数法求出抛物线的解析式;
(2)用含m的代数式分别表示出PE、EF,然后列方程求解;
(3)解题关键是识别出当四边形PECE′是菱形,然后根据PE=CE的条件,列出方程求解;当四边形PECE′是菱形不存在时,P点y轴上,即可得到m的值.
解:![]() ∵抛物线
∵抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,
两点,
∴![]() ,
,
解得![]() ,
,
∴抛物线的解析式为![]() .
.
![]() ∵点
∵点![]() 的横坐标为
的横坐标为![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
![]() .
.
由题意,![]() ,即:
,即:![]()
①若![]() ,整理得:
,整理得:![]() ,
,
解得:![]() 或
或![]() ;
;
②若![]() ,整理得:
,整理得:![]() ,
,
解得:![]() 或
或![]() .
.
由题意,![]() 的取值范围为:
的取值范围为:![]() ,故
,故![]() 、
、![]() 这两个解均舍去.
这两个解均舍去.
∴![]() 或
或![]() .
.
∴点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
![]() 假设存在.
假设存在.
作出示意图如下:
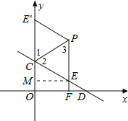
∵点![]() 、
、![]() 关于直线
关于直线![]() 对称,
对称,
∴![]() ,
,![]() ,
,![]() .
.
∵![]() 平行于
平行于![]() 轴,∴
轴,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,即四边形
,即四边形![]() 是菱形.
是菱形.
当四边形![]() 是菱形存在时,
是菱形存在时,
由直线![]() 解析式
解析式![]() ,可得
,可得![]() ,
,![]() ,由勾股定理得
,由勾股定理得![]() .
.
过点![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,易得
,易得![]() ,
,
∴![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴![]() ,又由
,又由![]() 可知:
可知:![]()
∴![]() .
.
①若![]() ,整理得:
,整理得:![]() ,解得
,解得![]() 或
或![]() ;
;
②若![]() ,整理得:
,整理得:![]() ,解得
,解得![]() ,
,![]() .
.
由题意,![]() 的取值范围为:
的取值范围为:![]() ,故
,故![]() 这个解舍去.
这个解舍去.
当四边形![]() 是菱形这一条件不存在时,
是菱形这一条件不存在时,
此时![]() 点横坐标为
点横坐标为![]() ,
,![]() ,
,![]() ,
,![]() 三点重合与
三点重合与![]() 轴上,也符合题意,
轴上,也符合题意,
∴![]() ,
,
综上所述,存在满足条件的![]() 的值为
的值为![]() 或
或![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目