Question

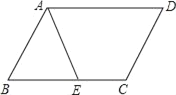
【题目】如图，在△ABC中，点D是BC的中点，点E、F分别是线段AD及其延长线上，且DE=DF，给出下列条件：①BE⊥EC；②BF∥EC；③AB=AC，从中选择一个条件使四边形BECF是菱形，并给出证明，你选择的条件是___（只填写序号）．

证明：

Answer 1

【答案】③，证明见解析

【解析】

根据点D是BC的中点可得DB=DC，且DE=DF，即可证明四边形BECF是平行四边形，然后根据菱形的判定定理即可作出判断．

证明：∵点D是BC的中点

∴BD=CD，

又∵DE=DF，

∴四边形BECF是平行四边形，

①BE⊥EC时，平行四边形BECF是矩形，不一定是菱形；
②四边形BECF是平行四边形，则BF∥EC一定成立，故不一定是菱形；
③AB=AC时，

∵AB=AC, 点D是BC的中点

∴

即

∴四边形BECF是菱形．

故选择的条件是③．