Question

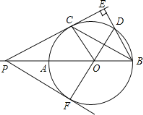
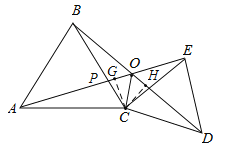
【题目】如图，△ABC、△CDE均为等边三角形，连接BD、AE交于点O，BC与AE交于于点P．

（1）求证：△ACE ≌ △BCD．

（2）求∠AOB的度数．

（3）连接OC，求证：OC平分∠AOD

Answer 1

【答案】(1)证明见解析；（2）；（3）证明见解析.

【解析】

（1）利用等边三角形的性质证明；

（2）由得到∠CBD=∠CAE．再利用三角形内角和等于180°，由△APC和△BPO中有内角互为对顶角进而得出∠BOA=∠ACP=60°.

（3）过C点作CG⊥AE，CH⊥BD，由三角形全等可得其对应高相等．再根据到角两边距离相等的点在角平分线即可得出结论.

（1）证明：与都是等边三角形，

，，，

∴，

即．

在和中，

，

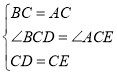（SAS）．

（2）．

∴∠CBD=∠CAE，
∵∠BPO =∠APC，

又∵∠CBD+∠BPO+∠BOP=∠CAE+∠APC+∠ACP=180°.
∴∠BOP=∠ACP=60°，即∠AOB=60°．

（3）如图，过C点作CG⊥AE，CH⊥BD，

，

∴，AE=BD，

∴，

∴CG=CH，

又∵CG⊥AE，CH⊥BD，

∴OC是∠AOD的角平分线，即OC平分∠AOD.