题目内容
3.在平面直角坐标系中,O为坐标原点,点A(a,a)在第一象限,点B(0,3),点C(c,0),其中0<c<3,∠BAC=90°.(1)根据题意,画出示意图;
(2)若a=2,求OC的长;
(3)已知点D在线段OC上,若OB2-OC2=8S△CAD,四边形OBAD的面积为$\frac{45}{8}$,求a2-a的值.
分析 (1)根据题意画出图形即可;
(2)由勾股定理表示出BC2=c2+9,AC2=(2-c)2+4,AB2=1+4=5,根据AB2+AC2=BC2,即5+(2-c)2+4=c2+9,解之可得c的值;
(3)过点A作AE⊥x轴于点E,作AF⊥y轴于点F,OF=OE=AF=AE=a,∠AEC=∠AFB=90°,由△ACE≌△ABF知BF=CE=3-a、OC=2a-3,根据OB2-OC2=8S△CAD得CD=3-a、OD=OC-CD=3a-6,最后由S四边形OBAD=S△OAB+S△OAD可得关于a的方程,变形可得答案.
解答 解:(1)如图,
(2)若a=2,则A(2,2),
连接BC,则BC2=c2+9,AC2=(2-c)2+4,AB2=1+4=5,
∵∠BAC=90°,
∴AB2+AC2=BC2,即5+(2-c)2+4=c2+9,
解得:c=1,
即OC=1;
(3)过点A作AE⊥x轴于点E,作AF⊥y轴于点F,
则OF=OE=AF=AE=a,∠AEC=∠AFB=90°,
∵∠CAE+∠ACF=90°,∠BAF+∠CAF=90°,
∴∠CAE=∠BAF,
在△ACE和△ABF中,
∵$\left\{\begin{array}{l}{∠AEC=∠AFB}\\{∠CAE=∠BAF}\\{AE=AF}\end{array}\right.$,
∴△ACE≌△ABF(AAS),
∴BF=CE=3-a,
∴OC=2a-3,
∵OB2-OC2=8S△CAD,
∴12a-4a2=8×$\frac{1}{2}$×CD×a,
∴CD=3-a,
∴OD=OC-CD=3a-6,
∵S四边形OBAD=S△OAB+S△OAD,
∴$\frac{45}{8}$=$\frac{3}{2}$a+$\frac{1}{2}$(3a-6)a,
∴a2-a=$\frac{15}{4}$
点评 本题主要考查坐标与图形的性质,熟练掌握勾股定理、全等三角形的判定与性质及割补法表示多边形的面积是解题的关键.

 习题精选系列答案
习题精选系列答案| A. | (-2016,2017) | B. | (2016,-2017) | C. | (2016,2017) | D. | (-2016,-2017) |
| A. | 斜边与一条直角边对应成比例的两个直角三角形相似 | |
| B. | 两个等腰直角三角形相似 | |
| C. | 两边对应成比例且有一个角相等的两个三角形相似 | |
| D. | 各有一个角等于100°的两个等腰三角形相似 |
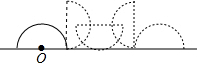 一个半圆形零件,直径紧贴地面,现需要将零件按如图所示方式,向前作无滑动翻转,使圆心O再次落在地面上止.已知半圆的半径为1m,则圆心O所经过的路线长是πm.(结果用π表示)
一个半圆形零件,直径紧贴地面,现需要将零件按如图所示方式,向前作无滑动翻转,使圆心O再次落在地面上止.已知半圆的半径为1m,则圆心O所经过的路线长是πm.(结果用π表示)

