题目内容
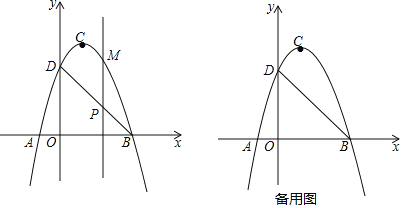
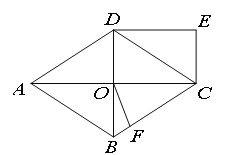
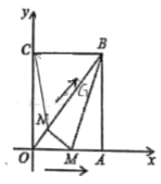
【题目】在直角坐标系中,已知抛物线![]() (a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知
(a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知![]() :S四边形ACBD=1:4.
:S四边形ACBD=1:4.
(1)求点D的坐标(用仅含c的代数式表示);
(2)若tan∠ACB=![]() ,求抛物线的解析式.
,求抛物线的解析式.
【答案】(1)D(2,![]() );(2)抛物线的解析式为:
);(2)抛物线的解析式为:![]() ,或
,或![]() ,或
,或![]() .
.
【解析】
(1)直接代入顶点坐标公式化简即可;
(2)先由![]() :S四边形ACBD=1:4,得到等底三角形的面积之比
:S四边形ACBD=1:4,得到等底三角形的面积之比![]() :
:![]() =1:3,而求出
=1:3,而求出![]() ,解析式化为
,解析式化为![]() ,求得A(1,0),B(3,0),过点B作
,求得A(1,0),B(3,0),过点B作![]() 的延长线于点H,得到
的延长线于点H,得到![]() ∽
∽![]() ,依据相似的性质、锐角三角函数,用c表示AH、BH,最后在三角形ABH中依据勾股定理求出c,即可得到解析式.
,依据相似的性质、锐角三角函数,用c表示AH、BH,最后在三角形ABH中依据勾股定理求出c,即可得到解析式.
解:(1)抛物线![]() 的顶点D的坐标为
的顶点D的坐标为![]()
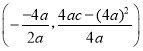 ,
,
∴顶点D的坐标为(2,![]() );
);
(2)∵![]() 与y轴负半轴交于点C,
与y轴负半轴交于点C,
∴C(0,c),![]() ,
,
过点D作![]() 轴于点G,则
轴于点G,则![]()
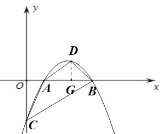
∵![]() :S四边形ACBD=1:4,
:S四边形ACBD=1:4,
∴![]() :
:![]() =1:3,
=1:3,
则![]() ,即
,即![]() ,
,
∴![]() ,
,
∴抛物线的解析式为:![]() 或
或![]() ,
,![]() =
=![]() ,
,![]() ,
,
∴令![]() =0,解得
=0,解得![]()
∴A(1,0),B(3,0),![]() ,
,
过点B作![]() 的延长线于点H,
的延长线于点H,

∴![]() (对顶角相等),
(对顶角相等),
∴![]() ∽
∽![]() ,tan∠ACB=
,tan∠ACB=![]() =
=![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∴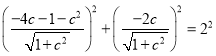 ,
,
∴![]() =0,(
=0,(![]() )
)
∴![]() -1或-3或-2+
-1或-3或-2+![]() (舍)或-2-
(舍)或-2-![]() ,
,
∴抛物线的解析式为:![]() ,或
,或![]() ,或
,或![]() .
.

练习册系列答案
相关题目