题目内容
【题目】在平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,,抛物线的顶点为点
,,抛物线的顶点为点![]() ,对称轴与
,对称轴与![]() 轴交于点
轴交于点![]() .
.

(1)求抛物线的表达式及点![]() 的坐标;
的坐标;
(2)点![]() 是
是![]() 轴正半轴上的一点,如果
轴正半轴上的一点,如果![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 是位于
是位于![]() 轴左侧抛物线上的一点,如果
轴左侧抛物线上的一点,如果![]() 是以
是以![]() 为直角边的直角三角形,求点
为直角边的直角三角形,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或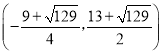
【解析】
(1)将点A、B 代入抛物线![]() ,即可求出抛物线解析式,再化为顶点式即可;
,即可求出抛物线解析式,再化为顶点式即可;
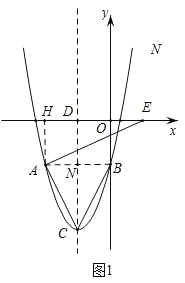
(2)如图1,连接AB,交对称轴于点N,则N(-![]() ,-2),利用相等角的正切值相等即可求出EH的长,OE的长,可写出点E的坐标;
,-2),利用相等角的正切值相等即可求出EH的长,OE的长,可写出点E的坐标;
(3)分∠EAP=90°和∠AEP=90°两种情况讨论,通过相似的性质,用含t的代数式表示出点P的坐标,可分别求出点P的坐标.
解:(1)(1)将点A(-3,-2)、B (0,-2)代入抛物线![]() ,
,
得,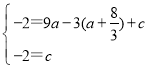 ,
,
解得,a=![]() ,c=-2,
,c=-2,
∴y=![]() x2+4x-2
x2+4x-2
=![]() (x+
(x+![]() )2-5,
)2-5,
∴抛物线解析式为y=![]() x2+4x-2,顶点C的坐标为(-
x2+4x-2,顶点C的坐标为(-![]() ,-5);
,-5);
(2)如图1,连接AB,交对称轴于点N,则N(-![]() ,-2),
,-2),
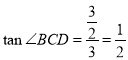 ,则
,则![]() ,
,
过![]() 作
作![]() ,
,![]() ,
,
则![]() ,
,
∵OH=3,
∴OE=1,
∴![]()
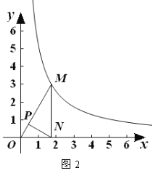
(3)①如图2,当∠EAP=90°时,
∵∠HEA+∠HAE=90,∠HAE+∠MAP=90°,
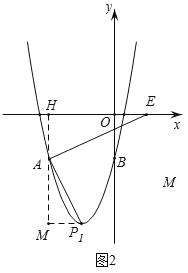
∴∠HEA=∠MAP,
又∠AHE=∠PMA=90°,
![]() ,
,
则![]() ,设
,设![]() ,则
,则![]()
将![]() 代入
代入![]()
得![]() (舍),
(舍),![]() ,
,
∴![]()
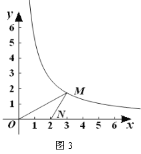
②如图3,当∠AEP=90°时,
∵∠EAG+∠AEG=90°,∠AEG+∠PEN=90°,
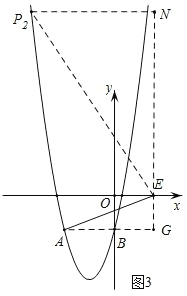
∴∠AEG=∠EPN,
又∵∠N=∠G=90°,
∴![]() ,则
,则![]()
设![]() ,则
,则![]()
将![]() 代入
代入![]()
得![]() ,
,![]() (舍),
(舍),
∴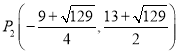
综上所述:![]() ,
,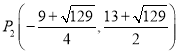

练习册系列答案
相关题目