Question

【题目】在正方形中，、分别为、的中点，连接、，和交于点．

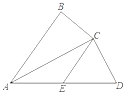
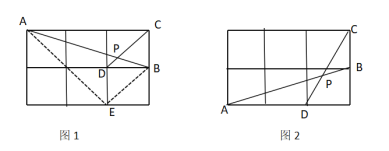
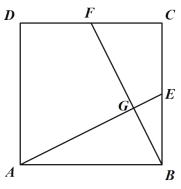
（1）如图1，求证：；

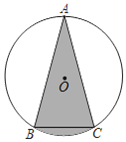
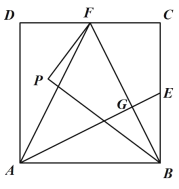
（2）如图2，作关于对称的图形，连接，在不添加任何辅助线的情况下，请直接写出图2中四个三角形，使写出的每个三角形的面积都等于正方形面积的．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

（1）依据正方形的性质，即可得到△ABE≌△BCF（SAS），进而得出∠BAE＝∠CBF，依据∠BGE＝90，即可得到AE⊥BF；

（2）依据E、F分别为BC、CD的中点，即可得到△ABE，△BCF，△BPF，△ADF的面积都等于正方形ABCD面积的．

（1）证明：如图1，∵、分别是正方形边、的中点，

∴，，，

∴

∴

∴

∵

∴

∴

∴

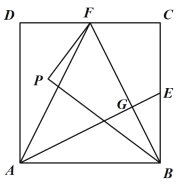
（2）如图2，

∵E、F分别为BC、CD的中点，

S△ABE=正方形ABCD，S△BCF=正方形ABCD，S△ADF=正方形ABCD，

∵作关于对称的图形

∴S△BPF=S△BCF=正方形ABCD，

∴的面积都等于正方形ABCD面积的．