题目内容
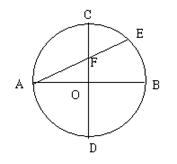
已知圆O的直径AB、CD互相垂直，弦AE交CD于F，若圆O的半径为R.求证：AE·AF＝2 R
.
证明：连接BE（1分）
，因为AB为圆O的直径，所以∠AEB=90°（2分）.因为AB⊥CD，所以∠AOF=90°，所以∠AOF=∠AEB=90°，又∠A=∠A，那么有△AOF∽△AEB（4分），所以
，则AE·AF=AO·AB，由于AO=R，AB=2R，所以有AE·AF=2R（7分）.
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
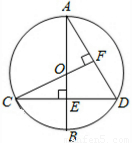
如图，已知圆O的直径AB垂直于弦CD于点E，连接CO并延长交AD于点F，且CF⊥AD．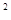
.
.
