题目内容
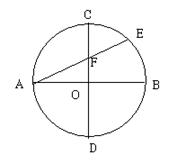
21.已知圆O的直径AB、CD互相垂直,弦AE交CD于F,若圆O的半径为R.
求证:AE·AF=2 R .
.
【答案】
见解析
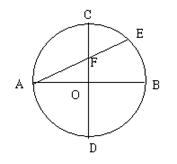
【解析】连接BE,根据圆周角定理可的∠AEB=90,再有AB⊥CD,公共角∠A,即可证得△AOF∽△AEB,根据相似三角形的对应边成比例即得结果。
解:如图,连接BE,

∵AB为⊙O的直径
∴∠AEB=90°
∵AB⊥CD
∴∠AOF=90°
∴∠AOF=∠AEB=90°
又∠A=∠A
∴△AOF∽△AEB
∴AE•AF=AO•AB
∵AO=R,AB=2R
所以AE•AF=2R2.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
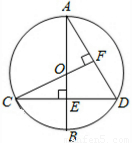
 如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD. .
.