Question

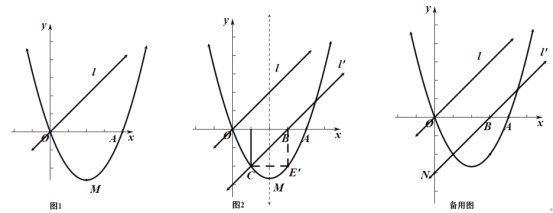
【题目】如图，分别过第二象限内的点作轴的平行线，与轴分别交于点与双曲线分别交于点

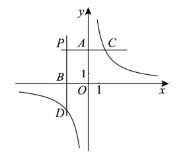
下面四个结论：

①存在无数个点使；

②存在无数个点使；

③至少存在一个点使；

④至少存在一个点使．

所有正确结论的序号是________．

Answer 1

【答案】①②④

【解析】

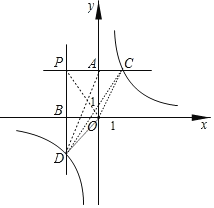
如图，设C（m，），D（n，），则P（n，），利用反比例函数k的几何意义得到S△AOC＝3，S△BOD＝3，则可对①进行判断；根据三角形面积公式可对②进行判断；通过计算S四边形OAPB和S△ACD得到m与n的关系可对对③进行判断．

解：如图，设C（m，），D（n，），则P（n，），

∵S△AOC＝，S△BOD＝，

∴S△AOC＝S△BOD；所以①正确；

∵S△POA＝，S△POB＝，

∴S△POA＝S△POB；所以②正确；

∵S△PCD＝，

∴当时，即3m2+4mn+3n2＝0，

∵△=42-4×3×3=-20＜0，

∴不存在点使；所以③错误；

∵S四边形OAPB＝﹣n×，S△ACD＝，

∴当时，即m2﹣mn﹣2n2＝0，

∴m＝2n（舍去）或m＝﹣n，此时P点为无数个，所以④正确．

故答案为：①②④．