Question

7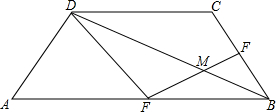．如图，梯形ABCD中，AB∥CD，且AB=2CD，E，F分别是AB，BC的中点，EF与BD相交于点M．
（1）证明：四边形EBCD是平行四边形；
（2）求$\frac{DM}{BM}$的值（未完成（1）可直接用（1）的结论）

Answer 1

分析 （1）由E是AB的中点，得出AB=2BF，再由已知条件得出CD∥BE，CD=BE，即可得出四边形EBCD是平行四边形；
（2）由平行四边形的性质得出DE=BC，DF∥BC，得出比例式$\frac{DM}{BM}=\frac{DF}{BF}$，由已知条件得出DF=2BF，即可得出结果．

解答 （1）证明：如图所示：
∵E是AB的中点，
∴AB=2BF，
∵AB∥CD，且AB=2CD，
∴CD∥BE，CD=BE，
∴四边形EBCD是平行四边形；
（2）解：∵四边形EBCD是平行四边形，
∴DE=BC，DF∥BC，
∴$\frac{DM}{BM}=\frac{DF}{BF}$，
∵F是BC的中点，
∴BC=2BF，
∴DF=2BF，
∴$\frac{DM}{BM}$=2．

点评 本题考查了梯形的性质、平行四边形的判定与性质、平行线分线段成比例定理；熟练掌握平行四边形的判定与性质，并能进行推理论证与计算是解决问题的关键．