题目内容
5.解下列方程(1)5x2-8x+2=0
(2)$\frac{x-2}{x+2}-\frac{16}{{{x^2}-4}}=\frac{x+2}{x-2}$.
分析 (1)首先确定a=5,b=-8,c=2,然后计算出△,再根据求根公式x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$计算出x的值即可;
(2)两边同时乘以(x+2)(x-2)得方程(x-2)(x-2)-16=(x+2)(x+2),再解整式方程即可,注意不要忘记检验.
解答 解:(1)5x2-8x+2=0,
a=5,b=-8,c=2,
△=b2-4ac=64-4×5×2=24>0,
则x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{8±2\sqrt{6}}{10}$=$\frac{{4±\sqrt{6}}}{5}$,
故x1=$\frac{4+\sqrt{6}}{5}$,x2=$\frac{4-\sqrt{6}}{5}$;
(2)两边同时乘以(x+2)(x-2)得:
(x-2)(x-2)-16=(x+2)(x+2),
解得:x=-2,
检验:当x=-2时,(x+2)(x-2)=0,
所以原方程无解.
点评 此题主要考查了公式法解二元一次方程,以及解分式方程,关键是掌握求根公式x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$,注意分式方程不要忘记检验.

练习册系列答案
相关题目
15.学校总务处与教务处各领了同样数量的信封和信笺,总务处每发出一封信都只用1张信笺,教务处每发出一封信都用3张信笺,结果,总务处用掉了所有的信封,但余下50张信笺;而教务处用掉了所有信笺,但余下50个信封.则两处所领的信笺张数、信封个数分别为( )
| A. | 150,100 | B. | 125,75 | C. | 120,70 | D. | 100,150 |
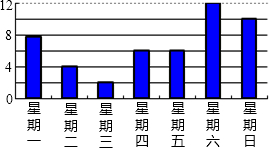 如图是明明作的一周的零用钱开支的统计图(单位:元)
如图是明明作的一周的零用钱开支的统计图(单位:元)  如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A-∠P=30°.
如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A-∠P=30°. 如图,是把一张长方形的纸片沿长边中点的连线对折两次后得到的图形,再沿虚线裁剪,展开后的图形是( )
如图,是把一张长方形的纸片沿长边中点的连线对折两次后得到的图形,再沿虚线裁剪,展开后的图形是( )



 如图,△ABC∽△BDC,BC=$\sqrt{6}$,AC=3,则CD=2.
如图,△ABC∽△BDC,BC=$\sqrt{6}$,AC=3,则CD=2.