题目内容
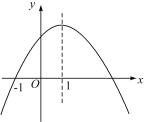
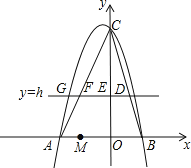
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,顶点为点
,顶点为点![]() .
.
(1)点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 ;(用含有
的坐标为 ;(用含有![]() 的代数式表示)
的代数式表示)
(2)连接![]() .
.
①若![]() 平分
平分![]() ,求二次函数的表达式;
,求二次函数的表达式;
②连接![]() ,若
,若![]() 平分
平分![]() ,求二次函数的表达式.
,求二次函数的表达式.
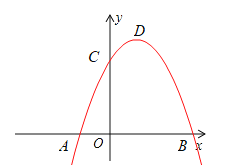
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ,②
,②![]()
【解析】
(1)令y=0,解关于x的方程,解方程即可求出x的值,进而可得点B的坐标;把抛物线的解析式转化为顶点式,即可得出点D的坐标;
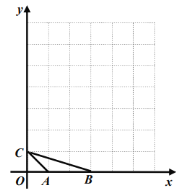
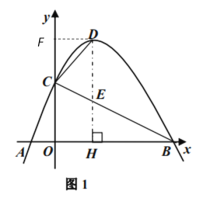
(2)①如图1,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,作DF⊥y轴于点F,则易得点C的坐标与CF的长,利用BH的长和∠B的正切可求出HE的长,进而可得DE的长,由题意和平行线的性质易推得
,作DF⊥y轴于点F,则易得点C的坐标与CF的长,利用BH的长和∠B的正切可求出HE的长,进而可得DE的长,由题意和平行线的性质易推得![]() ,然后可得关于m的方程,解方程即可求出m的值,进而可得答案;
,然后可得关于m的方程,解方程即可求出m的值,进而可得答案;
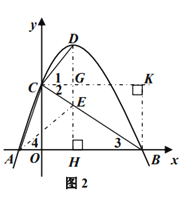
(3)如图2,过点B作BK∥y轴,过点C作CK∥x轴交BK于点K,交DH于点G,连接AE,利用锐角三角函数、抛物线的对称性和等腰三角形的性质可推出![]() ,进而可得
,进而可得![]() ,然后利用勾股定理可得关于m的方程,解方程即可求出m,问题即得解决.
,然后利用勾股定理可得关于m的方程,解方程即可求出m,问题即得解决.
解:(1)令y=0,则![]() ,
,
解得:![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
∵![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
故答案为:![]() ,
,![]() ;
;
(2)①如图1,过点![]() 作
作![]() 于点H,交
于点H,交![]() 于点
于点![]() ,作DF⊥y轴于点F,则
,作DF⊥y轴于点F,则![]() ,
,![]() ,DF=m,CF=
,DF=m,CF=![]() ,
,
∵![]() 平分
平分![]() ,
,
∴∠BCO=∠BCD,
∵DH∥OC,
∴∠BCO=∠DEC,
∴∠BCD=∠DEC,
∴![]() ,
,
∵![]() ,BH=2m,
,BH=2m,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() (
(![]() 舍去),
舍去),
∴二次函数的关系式为:![]() ;
;
②如图2,过点B作BK∥y轴,过点C作CK∥x轴交BK于点K,交DH于点G,连接AE,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵EA=EB,
∴∠3=∠4,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
解得:![]() (
(![]() 舍去),
舍去),
∴二次函数的关系式为:![]() .
.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目