题目内容
13.一元一次不等式组$\left\{\begin{array}{l}{3x+2>0}\\{x-4≤0}\end{array}\right.$的解集中,整数解的个数是( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
分析 先求出每个不等式的解集,再求出不等式组的解集,最后求出整数解即可.
解答 解:$\left\{\begin{array}{l}{3x+2>0①}\\{x-4≤0②}\end{array}\right.$
∵解不等式①得:x>-$\frac{2}{3}$,
解不等式②得:x≤4,
∴不等式组的解集为-$\frac{2}{3}$<x≤4,
∴不等式组的整数解为0,1,2,3,4,共5个,
故选B.
点评 本题考查了一元一次不等式组的整数解,解一元一次不等式组等知识点,能求出不等式组的解集是解此题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
3. 有理数a、b在数轴上的位置如图所示,则正确的式子是( )
有理数a、b在数轴上的位置如图所示,则正确的式子是( )
 有理数a、b在数轴上的位置如图所示,则正确的式子是( )
有理数a、b在数轴上的位置如图所示,则正确的式子是( )| A. | a>b | B. | a>-b | C. | -a<-b | D. | a<b |
1.“养生薪春,中国艾都”,我县今年6月获得“中国艾都”称号,其中我县某公司生产的“时珍牌”艾条畅销国内外,该公司生产的艾条每盒成本为20元,其销售y(万盒)与销售价格x(元/盒)的变化如下表,销售过程中的其他开支(不含成本)总计40万元.
(1)观察并分析表格中y与x的对应关系,用学过的函数知识写出y与x的函数解析式;
(2)求出该公司生产,销售这种艾条的净利润z(万元)与销售价格x(元/盒)的函数关系式,并求出销售价格定位多少时净利润最大?最大值是多少?
(3)改公司要求净利润不低于40万元,请写出销售价格x(元/盒)的取值范围.
| 价格x(元/盒) | … | 30 | 40 | 50 | 60 | … |
| 销售量y(万盒) | … | 5 | 4 | 3 | 2 | … |
(2)求出该公司生产,销售这种艾条的净利润z(万元)与销售价格x(元/盒)的函数关系式,并求出销售价格定位多少时净利润最大?最大值是多少?
(3)改公司要求净利润不低于40万元,请写出销售价格x(元/盒)的取值范围.
8.4的算术平方根是( )
| A. | 2 | B. | $\sqrt{2}$ | C. | -2 | D. | ±2 |
18. 如图,梯形ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线BD折叠,点A恰好落在DC边上的点A’处,若∠ABD=25°,则∠A′BC的度数为( )
如图,梯形ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线BD折叠,点A恰好落在DC边上的点A’处,若∠ABD=25°,则∠A′BC的度数为( )
 如图,梯形ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线BD折叠,点A恰好落在DC边上的点A’处,若∠ABD=25°,则∠A′BC的度数为( )
如图,梯形ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线BD折叠,点A恰好落在DC边上的点A’处,若∠ABD=25°,则∠A′BC的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
2.下列计算正确的是( )
| A. | a2+a3=a5 | B. | a2•a3=a6 | C. | (a2)3=a5 | D. | (-3x2y)3=-27x6y3 |
3.已知关于x的不等式组$\left\{\begin{array}{l}{\frac{x-1}{|x|}<0}\\{2x+1>a}\end{array}\right.$有且只有一个整数解,则a的取值范围是( )
| A. | -1<a≤1 | B. | -1≤a<1 | C. | -3<a≤-1 | D. | -3≤a<-1 |
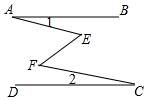 已知AB∥CD,∠AEF=∠EFC,探究:∠1与∠2的大小关系,并说明道理.
已知AB∥CD,∠AEF=∠EFC,探究:∠1与∠2的大小关系,并说明道理.