题目内容
7.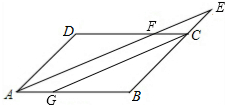 如图,在平行四边形中,F是DC上的一点,直线AF与BC的延长线交于点E,CG∥AE并与AB交于点G,下列式子中错误的是( )
如图,在平行四边形中,F是DC上的一点,直线AF与BC的延长线交于点E,CG∥AE并与AB交于点G,下列式子中错误的是( )| A. | $\frac{BC}{BE}$=$\frac{BG}{AB}$ | B. | $\frac{EF}{AE}$=$\frac{AG}{AB}$ | C. | $\frac{EF}{AF}$=$\frac{AG}{BG}$ | D. | $\frac{AF}{AE}$=$\frac{AG}{AB}$ |
分析 由平行四边形的性质得出AB∥CD,AD∥BE,证明四边形AGCF是平行四边形,△BCG∽△BEA,△CEF∽△BEA,得出$\frac{BC}{BE}=\frac{BG}{AB}$,$\frac{EF}{AE}=\frac{CF}{AB}$,CF=AG,证出DF=BG,得出选项A、B正确;由平行线证出$\frac{EF}{AF}=\frac{CF}{DF}$,得出$\frac{EF}{AF}=\frac{AG}{BG}$,得出选项C正确,D不正确;即可得出结论.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BE,
∵CG∥AE,
∴四边形AGCF是平行四边形,△BCG∽△BEA,△CEF∽△BEA,
∴$\frac{BC}{BE}=\frac{BG}{AB}$,$\frac{EF}{AE}=\frac{CF}{AB}$,CF=AG,
∴DF=BG,$\frac{EF}{AE}=\frac{AG}{AB}$,
∴选项A、B正确;
∵AD∥BE,
∴$\frac{EF}{AF}=\frac{CF}{DF}$,
∴$\frac{EF}{AF}=\frac{AG}{BG}$,
∴选项C正确,D不正确;
故选:D.
点评 本题考查了平行四边形的性质与判定、相似三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形相似得出比例式是解决问题的关键.

练习册系列答案
相关题目
19.在平面直角坐标系中,直线y=kx-k的图象可能是( )
| A. |  | B. |  | C. |  | D. |  |
16.已知在函数y=kx+b,其中常数k>0、b<0,那么这个函数的图象不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
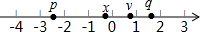 x、y、p、q在数轴上的位置如图所示,则点($\frac{x+1}{y}$,$\frac{p+2}{q}$)在平面直角坐标系xOy的第四象限.
x、y、p、q在数轴上的位置如图所示,则点($\frac{x+1}{y}$,$\frac{p+2}{q}$)在平面直角坐标系xOy的第四象限.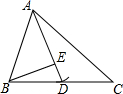 如图,在△ABC中,AC>AB,以点A为圆心、AB长为半径的弧恰交BC于点D,连接AD,过点B作BE⊥AD,垂足为E.
如图,在△ABC中,AC>AB,以点A为圆心、AB长为半径的弧恰交BC于点D,连接AD,过点B作BE⊥AD,垂足为E.