题目内容
12.△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于D,垂足为E,BD=10厘米,则AC=5厘米.分析 连接AD,根据线段垂直平分线的性质求出AD=BD=10厘米,求出∠BAD=∠B=15°,根据三角形外角性质求出∠CDA=∠B+∠BAD=30°,根据含30°角的直角三角形性质求出AC=$\frac{1}{2}$AD,代入求出即可.
解答 解:
连接AD,
∵AB的垂直平分线交BC于D,垂足为E,BD=10厘米,
∴AD=BD=10厘米,
∴∠B=∠BAD,
∵∠B=15°,
∴∠BAD=∠B=15°,
∴∠CDA=∠B+∠BAD=30°,
∴AC=$\frac{1}{2}$AD=$\frac{1}{2}×$10厘米=5厘米
故答案为:5厘米.
点评 本题考查了等腰三角形的性质,线段垂直平分线的性质,三角形外角性质,含30°角的直角三角形性质的应用,能综合运用性质进行推理是解此题的关键.

练习册系列答案
相关题目
3.下列变量之间的关系:
(1)凸多边形的对角线条数与边数;
(2)三角形面积与它的底边(高为定值);
(3)x-y=3中的x与y;
(4)圆的面积与圆的半径;
(5)y=|x|中的x与y.
其中成函数关系的有( )
(1)凸多边形的对角线条数与边数;
(2)三角形面积与它的底边(高为定值);
(3)x-y=3中的x与y;
(4)圆的面积与圆的半径;
(5)y=|x|中的x与y.
其中成函数关系的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
20.已知23×83=2n,则n的值为( )
| A. | 18 | B. | 7 | C. | 8 | D. | 12 |
 列方程解应用题:如图,利用一面长度为9m的墙,用18m长的篱笆,怎样围成一个面积为40m2的矩形场地?
列方程解应用题:如图,利用一面长度为9m的墙,用18m长的篱笆,怎样围成一个面积为40m2的矩形场地?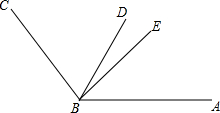 如图,BD平分∠ABC,BE将∠ABC分成3:5两部分,∠DBE=15°,求∠ABC的度数.
如图,BD平分∠ABC,BE将∠ABC分成3:5两部分,∠DBE=15°,求∠ABC的度数.