题目内容
4.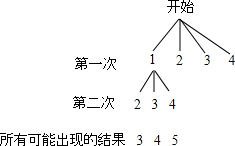 在不透明的袋子中有四张标着数字1,2,3,4 的卡片,这些卡片除数字外都相同.甲同学按照一定的规则抽出两张卡片,并把卡片上的数字相加.如图是他所画的树状图的一部分.
在不透明的袋子中有四张标着数字1,2,3,4 的卡片,这些卡片除数字外都相同.甲同学按照一定的规则抽出两张卡片,并把卡片上的数字相加.如图是他所画的树状图的一部分.(1)由如图分析,甲同学的游戏规则是:从袋子中随机抽出一张卡片后不放回(填“放回”或“不放回”),再随机抽出一张卡片;
(2)帮甲同学完成树状图;
(3)求甲同学两次抽到的数字之和为偶数的概率.
分析 (1)根据小明画出的树形图知数字1在第一次中出现,但没有在第二次中出现可以判断;
(2)根据本实验是一个不放回试验作出树状图即可;
(3)根据树状图利用概率公式求解即可.
解答 解:(1)观察树状图知:第一次摸出的数字没有在第二次中出现,
∴甲同学的实验是一个不放回实验,
故答案为:不放回;
(2)补全树状图为:
(3)由树状图得:
共有12种情况,两次抽到的数字之和为偶数的有4种,
故P(两次抽到的数字之和为偶数)=$\frac{4}{12}$=$\frac{1}{3}$.
点评 本题考查了列表法和树状图法,利用列表法或树状图法展示某一随机事件中所有等可能出现的结果数n,再找出其中某一事件所出现的可能数m,然后根据概率的定义可计算出这个事件的概率$\frac{m}{n}$.

练习册系列答案
相关题目
15.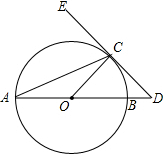 如图,AB⊙O的直径,ED切⊙O于点C,交AB的延长线于点D,且CO=CD,则∠ECA=( )
如图,AB⊙O的直径,ED切⊙O于点C,交AB的延长线于点D,且CO=CD,则∠ECA=( )
 如图,AB⊙O的直径,ED切⊙O于点C,交AB的延长线于点D,且CO=CD,则∠ECA=( )
如图,AB⊙O的直径,ED切⊙O于点C,交AB的延长线于点D,且CO=CD,则∠ECA=( )| A. | 30° | B. | 45° | C. | 60° | D. | 67.5° |
16.与-2的差为0的数是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
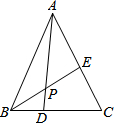 如图,在△ABC中,BD:DC=1:2,E是AC的中点,AD与BE相交于点P,P恰为BE中点,则AP:PD=3:1.
如图,在△ABC中,BD:DC=1:2,E是AC的中点,AD与BE相交于点P,P恰为BE中点,则AP:PD=3:1.