题目内容
20．如图，边长为1的正方形，经过一次生长后，在它的左右肩上生出两个小正方形，如图1，其中，三个正方形围成的三角形是直角三角形．再经过一次“生长”后，变成图2；如果继续“生长”下去，它将变得更加“枝繁叶茂”． 请你算出“生长”了2014次后形成的图形中，所有的正方形的面积和是2015．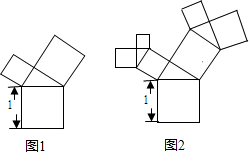
分析 求出每一次生长后所生长出的四边形面积，找出变化规律，计算出所有四边形的面积．
解答 
解：如图，第一次生长后长出的三角形面积为SA+SB=1；
第二次生长后长出的三角形面积为SD+SC+SA+SB=1；
第三次生长后长出的三角形面积为：1；
第四次生长后长出的三角形面积为：1；
…
“生长”了2014次后形成的图形中，所有的正方形的面积和是1×2014+1=2015．
故答案为2015．
点评 本题考查了勾股定理，熟悉勾股定理的几何意义是解题的关键．
练习册系列答案
相关题目
如图所示，直线CD、EF被直线AB所截，若∠AMC=∠BNF，则∠CMN+∠MNE=180°．
15．$\sqrt{43}$介于哪两个整数之间（ ）
| A． | 4与5 | B． | 5与6 | C． | 6与7 | D． | 7与8 |
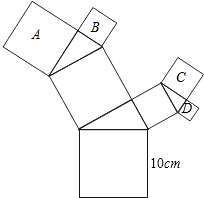如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为10cm，正方形A的边长为5cm、B的边长为6cm、C的边长为5cm，则正方形D的边长为$\sqrt{14}$cm．