题目内容
 如图,BF是∠DBC的平分线,CF是∠ECB的平分线,点F在∠BAC的平分线上吗?证明你的结论.
如图,BF是∠DBC的平分线,CF是∠ECB的平分线,点F在∠BAC的平分线上吗?证明你的结论.考点:角平分线的性质
专题:
分析:过点F作FG⊥AB的延长线于G,作FH⊥AC的延长线于H,作FK⊥BC于K,根据角平分线上的点到角的两边距离相等可得FG=FK,FK=FH,然后求出FG=FH,再根据到角的两边距离相等的点在角的平分线上证明.
解答: 证明:如图,过点F作FG⊥AB的延长线于G,作FH⊥AC的延长线于H,作FK⊥BC于K,
证明:如图,过点F作FG⊥AB的延长线于G,作FH⊥AC的延长线于H,作FK⊥BC于K,
∵BF是∠DBC的平分线,
∴FG=FK,
∵CF是∠ECB的平分线,
∴FK=FH,
∴FG=FH,
∴点F在∠BAC的平分线上.
 证明:如图,过点F作FG⊥AB的延长线于G,作FH⊥AC的延长线于H,作FK⊥BC于K,
证明:如图,过点F作FG⊥AB的延长线于G,作FH⊥AC的延长线于H,作FK⊥BC于K,∵BF是∠DBC的平分线,
∴FG=FK,
∵CF是∠ECB的平分线,
∴FK=FH,
∴FG=FH,
∴点F在∠BAC的平分线上.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,到角的两边距离相等的点在角的平分线上,熟记性质与角的平分线的判定是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列运算正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|

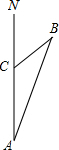 一船上午9时从海岛A出发一20海里/时的速度向正北方向向航行,11时到达B处,从A,B两处分别望灯塔C,测得∠NBA=30°,∠NCB=45°,求从B处到灯塔C的距离.
一船上午9时从海岛A出发一20海里/时的速度向正北方向向航行,11时到达B处,从A,B两处分别望灯塔C,测得∠NBA=30°,∠NCB=45°,求从B处到灯塔C的距离.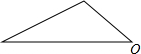 在一次黑板报的评选中,九年级(1)班获得了第一名,其中小颖同学的图案得到了大家的一致好评.她设计的图案是由如图所示的三角形图案绕上面的点O按同一个方向依次旋转90°,180°,270°得到的图形组成的,请你画出这个图案,并描述这个图案像什么.
在一次黑板报的评选中,九年级(1)班获得了第一名,其中小颖同学的图案得到了大家的一致好评.她设计的图案是由如图所示的三角形图案绕上面的点O按同一个方向依次旋转90°,180°,270°得到的图形组成的,请你画出这个图案,并描述这个图案像什么. 已知直线a,b,过a上一点A作AB⊥a,交b于点B,过B作BC⊥b交a于点C.则点B到直线a的距离是
已知直线a,b,过a上一点A作AB⊥a,交b于点B,过B作BC⊥b交a于点C.则点B到直线a的距离是 如图,已知∠1=∠2,∠B=80°,求∠BCD的度数.
如图,已知∠1=∠2,∠B=80°,求∠BCD的度数.