题目内容
5．将下列各式因式分解：（1）（x+y）2-9y2；
（2）（x-y）3+4（y-x）．
分析 （1）原式利用平方差公式分解即可；
（2）原式变形后，提取公因式，再利用平方差公式分解即可．
解答 解：（1）原式=（x+y+3y）（x+y-3y）=（x+4y）（x-2y）；
（2）原式=（x-y）3-4（x-y）=（x-y）[（x-y）2-4]=（x-y）（x-y+2）（x-y-2）．
点评 此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
相关题目
15．
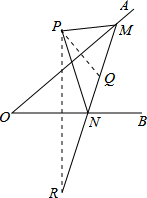如图，点P是∠AOB外的一点，点M，N分别是∠AOB两边上的点，点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在MN的延长线上．若PM=3cm，PN=4cm，MN=4.5cm，则线段QR的长为（ ）
如图，点P是∠AOB外的一点，点M，N分别是∠AOB两边上的点，点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在MN的延长线上．若PM=3cm，PN=4cm，MN=4.5cm，则线段QR的长为（ ）| A． | 4.5 | B． | 5.5 | C． | 6.5 | D． | 7 |
16．对于反比例函数y=$\frac{3}{x}$，下列判断正确的是（ ）
| A． | 图象经过点（-1，3） | |
| B． | 图象在第二、四象限 | |
| C． | 不论x为何值，y＞0 | |
| D． | 图象所在的第一象限内，y随x的增大而减小 |
如图所示，P为△AOB内一点，M、N分别为OA、OB上任意点，∠MPN=β，∠AOB=α，当△MPN的周长最小时，求α，β的关系．