题目内容
15.已知1<x<8,化简$\sqrt{{x}^{2}-16x+64}$+$\sqrt{{x}^{2}+16x+64}$+$\frac{|1-x|}{x-1}$.分析 根据$\sqrt{{a}^{2}}$=|a|进行化简,然后合并同类项即可.
解答 解:∵1<x<8,
∴$\sqrt{{x}^{2}-16x+64}$+$\sqrt{{x}^{2}+16x+64}$+$\frac{|1-x|}{x-1}$
=|x-8|+|x+8|+$\frac{|1-x|}{x-1}$
=8-x+x+8-1
=15.
点评 本题考查的是二次根式的性质和化简,掌握$\sqrt{{a}^{2}}$=|a|是解题的关键.

练习册系列答案
相关题目
6.下列数组中是勾股数的是( )
| A. | 6,8,9 | B. | 7,15,17 | C. | 7,24,26 | D. | 5,12,13 |
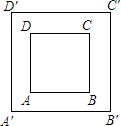 如图,有一块矩形草坪,沿草坪四周有宽为3m的环形小路.
如图,有一块矩形草坪,沿草坪四周有宽为3m的环形小路.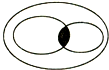 从知识结构来看,平行四边形、矩形、菱形、正方形的包含关系可以如图表示,则其中最大的椭圆表示的是平行四边形,阴影部分表示的是正方形.
从知识结构来看,平行四边形、矩形、菱形、正方形的包含关系可以如图表示,则其中最大的椭圆表示的是平行四边形,阴影部分表示的是正方形.