题目内容
10.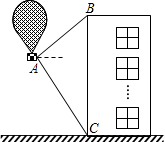 “五一”节期间在我市市民广场进行了热气球飞行表演,如图,有一热气球到达离地面高度为36米的A处时,仪器显示如图,有一热气球到达离地面高度为36米的A处时,仪器显正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)
“五一”节期间在我市市民广场进行了热气球飞行表演,如图,有一热气球到达离地面高度为36米的A处时,仪器显示如图,有一热气球到达离地面高度为36米的A处时,仪器显正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,$\sqrt{3}$≈1.73)
分析 过点A作AD⊥BC于D,在Rt△ACD中求出AD,在Rt△ABD中求出BD,继而可得出答案.
解答 解:如图,过点A作AD⊥BC于D,
在Rt△ACD中,∠2=60°,CD=36米,
∵tan∠2=$\frac{CD}{AD}$,
∴AD=CD÷tan∠2=36÷$\sqrt{3}$=12$\sqrt{3}$米,
在Rt△ABD中,∵∠1=37°,
∴BD=ADtan37°=12$\sqrt{3}$×0.75≈12×1.73≈15.6米.
答:为了安全飞越高楼,气球应至少再上升15.6米.
点评 本题考查了解直角三角形的应用,构造直角三角形是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
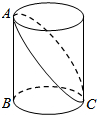 如图,已知圆柱底面的周长为4dm,圆柱高为2dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为4$\sqrt{2}$dm.
如图,已知圆柱底面的周长为4dm,圆柱高为2dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为4$\sqrt{2}$dm.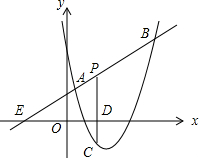 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( $\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( $\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C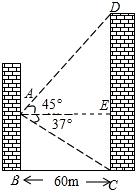 如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部的仰角是45°,而大厦底部的俯角是37°,求该大厦的高度(结果精确到0.1米)
如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部的仰角是45°,而大厦底部的俯角是37°,求该大厦的高度(结果精确到0.1米)
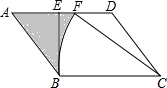 如图,平行四边形ABCD中,BE⊥AD于点E,以C为圆心,BC长为半径画弧,恰好过AD的中点F,若BC=4,BE=2,则图中阴影部分的面积为6-$\frac{4}{3}$π.
如图,平行四边形ABCD中,BE⊥AD于点E,以C为圆心,BC长为半径画弧,恰好过AD的中点F,若BC=4,BE=2,则图中阴影部分的面积为6-$\frac{4}{3}$π.