题目内容
1.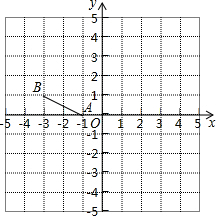 如图已知A点坐标为(-1,0),B点(-3,1).
如图已知A点坐标为(-1,0),B点(-3,1).(1)将点A绕着点B逆时针旋转90°得到点C,请在方格纸中画出△ABC;
(2)将△ABC平移得三角形△DEF,使得点A与D对应,点B与E对应,点C与F对应,其中点D的坐标为(4,1)画出△DEF;
(3)△ABC平移的距离为$\sqrt{26}$;
(4)连接AD、CF,四边形ADFC面积为16.
分析 (1)由旋转的定义即可得;
(2)根据点A(-1,0)的对应点D(4,1),得出需将△ABC向右平移5格、向上平移1格,据此可得△DEF;
(3)根据勾股定理求出AD的长即可;
(4)割补法求解可得.
解答 解:(1)由旋转的定义得出点C,顺次连接即可得△ABC;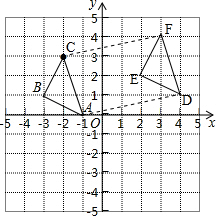
(2)如图,△DEF即为所求;
(3)△ABC平移的距离AD=$\sqrt{{5}^{2}+{1}^{2}}$=$\sqrt{26}$,
故答案为:$\sqrt{26}$;
(4)四边形ADFC面积为4×6-2×$\frac{1}{2}$×1×5-2×$\frac{1}{2}$×1×3=16,
故答案为:16.
点评 本题主要考查作图-旋转变换、平移变换,熟练掌握旋转变换、平移变换的定义及其性质、勾股定理、割补法求面积是解题的关键.

练习册系列答案
相关题目
11.一元二次方程x2-6x-10=0配方后可变形为( )
| A. | (x-3)2=19 | B. | (x-3)2=1 | C. | (x+3)2=19 | D. | (x+3)2=1 |
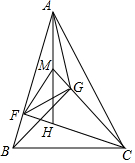 如图,△ABC为锐角三角形,CF⊥AB于F,H为△ABC的垂心.M为AH的中点,点G在线段CM上,且CG⊥GB.
如图,△ABC为锐角三角形,CF⊥AB于F,H为△ABC的垂心.M为AH的中点,点G在线段CM上,且CG⊥GB.