题目内容
 如图,直线
如图,直线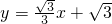 与x轴、y分别相交与A、B两点,圆心P的坐标为(1,0),圆P与y轴相切与点O.若将圆P沿x轴向左移动,当圆P与该直线相交时,令圆心P的横坐标为m,则m的取值范围是________.
与x轴、y分别相交与A、B两点,圆心P的坐标为(1,0),圆P与y轴相切与点O.若将圆P沿x轴向左移动,当圆P与该直线相交时,令圆心P的横坐标为m,则m的取值范围是________.
-5<m<-1
分析:求出函数与x轴、y轴的交点坐标,求出函数与x轴的夹角,计算出当⊙P与AB线切时点P的坐标,判断出P的横坐标的取值范围.
解答: 解:令y=0,则
解:令y=0,则 x+
x+ =0,
=0,
解得x=-3,
则A点坐标为(-3,0);
令x=0,则y= ,
,
则B点坐标为(0, ),
),
则tan∠BAO= ,
,
则∠BAO=30°,
作⊙P′与⊙P″切AB于D、E,
连接P′D、P″E,则P′D⊥AB、P″E⊥AB,
则在Rt△ADP′中,AP′=2×DP′=2,
同理可得,AP″=2,
则P′横坐标为-3+2=-1,P″横坐标为-1-4=-5,
故P横坐标m的取值范围为:-5<m<-1,
故答案为:-5<m<-1
点评:本题考查了一次函数综合题,涉及的知识有:一次函数的图象与性质,切线的性质,一次函数与坐标轴的交点,以及坐标与图形性质,熟悉一次函数的性质和切线的性质是解题的关键.
分析:求出函数与x轴、y轴的交点坐标,求出函数与x轴的夹角,计算出当⊙P与AB线切时点P的坐标,判断出P的横坐标的取值范围.
解答:
 解:令y=0,则
解:令y=0,则 x+
x+ =0,
=0,解得x=-3,
则A点坐标为(-3,0);
令x=0,则y=
 ,
,则B点坐标为(0,
 ),
),则tan∠BAO=
 ,
,则∠BAO=30°,
作⊙P′与⊙P″切AB于D、E,
连接P′D、P″E,则P′D⊥AB、P″E⊥AB,
则在Rt△ADP′中,AP′=2×DP′=2,
同理可得,AP″=2,
则P′横坐标为-3+2=-1,P″横坐标为-1-4=-5,
故P横坐标m的取值范围为:-5<m<-1,
故答案为:-5<m<-1
点评:本题考查了一次函数综合题,涉及的知识有:一次函数的图象与性质,切线的性质,一次函数与坐标轴的交点,以及坐标与图形性质,熟悉一次函数的性质和切线的性质是解题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 如图,直线与x轴、y轴分别交于A、B两点.
如图,直线与x轴、y轴分别交于A、B两点.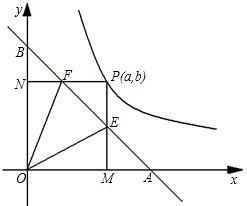
 3、如图,直线与y轴的交点是(0,-3),则当x<0时,( )
3、如图,直线与y轴的交点是(0,-3),则当x<0时,( ) 如图,直线与x轴、y轴分别交于A、B两点.
如图,直线与x轴、y轴分别交于A、B两点. 与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且
与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且 ,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.
,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.