题目内容
1. 如图,∠ABD和∠BDC两个角的平分线交于点E,DE的延长线交AB于F.
如图,∠ABD和∠BDC两个角的平分线交于点E,DE的延长线交AB于F.(1)如果∠1+∠2=90°,那么AB与CD平行吗?请说明理由;
(2)如果AB∥CD,那么∠2和∠3互余吗?请说明理由.
分析 (1)根据平行线的性质可得出∠ABD=2∠2,∠BDC=2∠1,再由∠1+∠2=90°可得出∠ABD+∠BDC=180°,依据“同旁内角互补,两直线平行”即可得出结论;
(2))根据平行线的性质可得出∠ABD=2∠2,∠BDC=2∠1,∠EBF=∠2,再由AB∥CD可得出∠ABD+∠BDC=180°,根据角的关系即可得出∠1+∠2=90°,结合直角三角形的性质及等量替换即可得出∠2+∠3=90°,此题得解.
解答 解:(1)平行,理由如下:
∵DE平分∠BDC,BE平分∠ABD,
∴∠ABD=2∠2,∠BDC=2∠1,
∵∠1+∠2=90°,
∴∠ABD+∠BDC=2×(∠1+∠2)=180°,
∴AB∥CD.
(2)互余,理由如下:
∵DE平分∠BDC,BE平分∠ABD,
∴∠ABD=2∠2,∠BDC=2∠1,∠EBF=∠2,
∵AB∥CD,
∴∠ABD+∠BDC=180°,
∴∠1+∠2=90°,
∴∠BED=90°,∠BEF=90°,
∴∠EBF+∠3=90°,
∴∠2+∠3=90°,
即∠2和∠3互余.
点评 本题考查了平行线段的判定及性质、余角和补角以及角的计算,解题的关键是:(1)找出∠ABD+∠BDC=180°;(2)找出∠2+∠3=90°.本题属于中档题,难度不大,解决该题型题目时,牢记平行线的判定及性质是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.据国家财政部估算,初步预计2009年全国财政收入将为65720亿元,用科学记数法表示为( )
| A. | 6.572×1010 | B. | 6.572×1011 | C. | 6.572×1012 | D. | 6.572×1013 |
9.我国研制的“曙光3000超级服务器”排在全世界运算速度最快的500台高性能计算机的第80位,它的峰值速度达到每秒403 200 000 000次,用科学记数法表示它的峰值计算速度为每秒( )次.
| A. | 0.4032×1012 | B. | 403.2×109 | C. | 4.032×108 | D. | 4.032×1011 |
13.若a>b,则下列不等式不一定成立的是( )
| A. | a+m>b+m | B. | a(m2+1)>b(m2+1) | C. | -2a<-2b | D. | a2>b2 |
10.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{xy=1}\\{x+2y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{3y-x=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{\frac{1}{x}+\frac{1}{y}=1}\\{x+y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+z=2}\\{x+y=3}\end{array}\right.$ |
4.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
若A(m,y1),B(m-2,y2)两点都在该函数的图象上,当m=3时,y1=y2.
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | 5 | … |
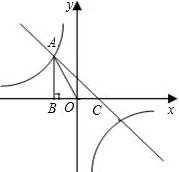 如图,已知反比例函数y=$\frac{k}{x}$(k<0)的图象经过点$A(-\sqrt{3},2)$,过点A作AB⊥x轴于点B,连结AO.
如图,已知反比例函数y=$\frac{k}{x}$(k<0)的图象经过点$A(-\sqrt{3},2)$,过点A作AB⊥x轴于点B,连结AO.