题目内容
6. 如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1).$\widehat{A{A}_{1}}$是以点B为圆心,BA为半径的圆弧;$\widehat{{A}_{1}{A}_{2}}$是以点O为圆心,OA1为半径的圆弧,$\widehat{{A}_{2}{A}_{3}}$是以点C为圆心,CA2为半径的圆弧,$\widehat{{A}_{3}{A}_{4}}$是以点A为圆心,AA3为半径的圆弧,继续以点B、O、C、A为圆心按上述作法得到的曲线AA1A2A3A4A5…称为“正方形的渐开线”,那么点A5的坐标是(6,0),点A2015的坐标是(-2015,1).
如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1).$\widehat{A{A}_{1}}$是以点B为圆心,BA为半径的圆弧;$\widehat{{A}_{1}{A}_{2}}$是以点O为圆心,OA1为半径的圆弧,$\widehat{{A}_{2}{A}_{3}}$是以点C为圆心,CA2为半径的圆弧,$\widehat{{A}_{3}{A}_{4}}$是以点A为圆心,AA3为半径的圆弧,继续以点B、O、C、A为圆心按上述作法得到的曲线AA1A2A3A4A5…称为“正方形的渐开线”,那么点A5的坐标是(6,0),点A2015的坐标是(-2015,1).
分析 点A的坐标为(1,1),则BA1=1,A1坐标为(2,0),依此类推,A2(0,-2),A3(-3,1),A4(1,5),A5是以B为圆心,BA4为半径的圆弧与x轴的交点,则A5(6,0),2015÷4=503…3,A2015应与A3(-3,1)的坐标规律一样,故A2015(-2015,1).
解答 解:∵点A的坐标为(1,1),四边形ABOC是正方形,
BA1=1,
∴A1坐标为(2,0),
∵$\widehat{{A}_{1}{A}_{2}}$是以点O为圆心,OA1为半径的圆弧,
∴A2(0,-2),
∵$\widehat{{A}_{2}{A}_{3}}$是以点C为圆心,CA2为半径的圆弧,
∴A3(-3,1),
∵$\widehat{{A}_{3}{A}_{4}}$是以点A为圆心,AA3为半径的圆弧,
∴A4(1,5),
依此类推,$\widehat{{A}_{4}{A}_{5}}$是以B为圆心,BA4为半径的圆弧与x轴的交点,
则A5(6,0),
A5(6,0)与A1(2,0)坐标规律相同,
∵2015÷4=503…3,
∴A2015应与A3(-3,1)的坐标规律一样,
故A2015(-2015,1).
故答案为:(6,0),(-2015,1).
点评 本题主要考查了点的坐标的变化规律和对“正方形的渐开线”的理解,发现规律,理解“正方形的渐开线”是解答此题的关键.

练习册系列答案
相关题目
17.方程x2-(m+6)x+m2=0有两个相等的实数根,则m的值是( )
| A. | -2或6 | B. | 6 | C. | -2 | D. | -6或2 |
16.一个不透明的袋中装有红、白、黄3种颜色的若干个小球,它们除颜色外完全相同.每次从袋中摸出1个球,记下颜色后放回搅匀再摸.摸球实验中,统计得到下表中的数据:
由此可以估计摸到黄球的概率约为0.4(精确到0.1).
| 摸球次数 | 10 | 20 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
| 出现红球的频数 | 4 | 9 | 16 | 31 | 44 | 61 | 74 | 92 | 118 | 147 |
| 出现白球的频数 | 1 | 4 | 16 | 36 | 52 | 61 | 75 | 85 | 123 | 151 |
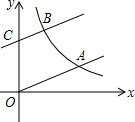 如图,一次函数y=$\frac{1}{3}$x的图象与反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象交于点A,将一次函数y=$\frac{1}{3}$x的图象向上平移3个单位得到一次函数y=ax+b的图象,它与y轴交于点C,与反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象交于点B,已知OA=2BC.
如图,一次函数y=$\frac{1}{3}$x的图象与反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象交于点A,将一次函数y=$\frac{1}{3}$x的图象向上平移3个单位得到一次函数y=ax+b的图象,它与y轴交于点C,与反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象交于点B,已知OA=2BC.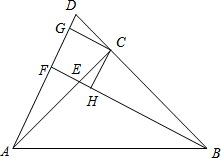 已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E在边AC上,延长BC至D点,使CE=CD,延长BE交AD于F,过点C作CG∥BF,交AD于点G,在BE上取一点H,使∠HCE=∠DCG.
已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E在边AC上,延长BC至D点,使CE=CD,延长BE交AD于F,过点C作CG∥BF,交AD于点G,在BE上取一点H,使∠HCE=∠DCG.