题目内容
23、如图所示，∠BAC=90°，BF平分∠ABC交AC于点F，∠BFC=100°，求∠C的度数．
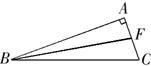
分析：根据角平分线的性质和外角与内角的关系，将问题转化为△ABC的内角和问题解答．
解答：解：∵∠BAC=90°，∠BFC=100°，∠BFC是△ABF的外角，
∴∠ABF=100°-90°=10°，
∵BF平分∠ABC交AC于点F，
∴∠ABC=2×∠ABF=2×10°=20°，
∴∠C=180°-90°-20°=70°．
∴∠ABF=100°-90°=10°，
∵BF平分∠ABC交AC于点F，
∴∠ABC=2×∠ABF=2×10°=20°，
∴∠C=180°-90°-20°=70°．
点评：此题巧妙结合了三角形内角和、三角形内角和外角的关系及角平分线的性质定理，解答时要注意将同一个角置于不同的三角形中分析．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
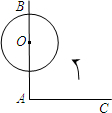如图所示，∠BAC=90°，O为AB上一点，以O为圆心，| 1 |
| 2 |
| A、30° | B、60° |
| C、60°或120° | D、120° |
5、如图所示，∠BAC=90°，AB=AC，过点A任意作一直线DE，且作CE⊥ED，BD⊥ED，经测量CE=2cm，BD=4cm，则DE的长为（ ）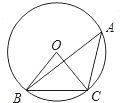
如图所示，∠BAC是⊙O的圆周角，则∠BAC+∠OCB=
19、如图所示，∠BAC=∠ABD，AC=BD，点O是AD、BC的交点，点E是AB的中点．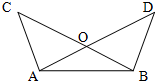
18、如图所示，∠BAC=∠ABD，AC=BD，点O是AD、BC的交点，