题目内容
4.计算:-2-2-20110-|-$\frac{4}{\sqrt{3}}$|+tan30°.分析 首先根据实数运算的方法,分别求出-2-2、20110、|-$\frac{4}{\sqrt{3}}$|、tan30°的值各是多少;然后从左向右依次计算,求出算式-2-2-20110-|-$\frac{4}{\sqrt{3}}$|+tan30°的值是多少即可.
解答 解:-2-2-20110-|-$\frac{4}{\sqrt{3}}$|+tan30°
=-$\frac{1}{4}-1-\frac{4\sqrt{3}}{3}+\frac{\sqrt{3}}{3}$
=-$\frac{5}{4}-\sqrt{3}$
点评 (1)此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到有的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
(2)此题还考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.
(3)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a0=1(a≠0);②00≠1.
(4)此题还考查了特殊角的三角函数值,要牢记30°、45°、60°角的各种三角函数值.

练习册系列答案
相关题目
19. 如图,点O为数轴原点,则数轴上表示互为相反数的点是( )
如图,点O为数轴原点,则数轴上表示互为相反数的点是( )
 如图,点O为数轴原点,则数轴上表示互为相反数的点是( )
如图,点O为数轴原点,则数轴上表示互为相反数的点是( )| A. | 点A和点C | B. | 点C和点D | C. | 点A和点D | D. | 点B和点D |
14.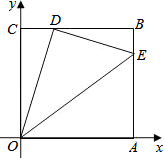 如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )
如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )
 如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )
如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
 如图,在正方形ABCD中,E在BC上.
如图,在正方形ABCD中,E在BC上. 如图,反比例函数y=$\frac{k}{x}$的图象经过矩形AOBC的边AC的中点E,与另一边BC交于点D,连接DE,若S△ECD=2,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$的图象经过矩形AOBC的边AC的中点E,与另一边BC交于点D,连接DE,若S△ECD=2,则k的值为( )