题目内容
16.已知抛物线y=a(x+m)2经过点(2,-2),且对称轴是过点(3,0)且平行于y轴的直线.(1)此函数的解析式;
(2)出此抛物线的开口方向、顶点坐标;
(3)函数有最大值还是最小值?
(4)把此抛物线向右平移2个单位得到的抛物线是什么?
分析 (1)由已知条件得出m=-3,然后把(2,-2)代入解析式即可求得a的值;
(2)根据(1)求得的解析式即可得出开口方向、顶点坐标;
(3)根据抛物线的性质即可求得;
(4)根据平移的性质即可求得.
解答 解:(1)∵抛物线y=a(x+m)2的对称轴是过点(3,0)且平行于y轴的直线.
∴m=-3,
把(2,-2)代入得,-2=a(2-3)2,
解得a=-2,
∴此函数的解析式为y=-2(x-3)2;
(2)由y=-2(x-3)2可知,抛物线开口向下,顶点为(3,0);
(3)∵抛物线的开口向下,
∴函数有最大值为0;
(4)∵此抛物线向右平移2个单位,
∴得到的抛物线是y=-2(x-5)2.
点评 本题考查了待定系数法求二次函数的解析式,二次函数的性质,二次函数图象与几何变换,熟练掌握待定系数法求得解析式是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
4.下列各式中,计算结果为正的是( )
| A. | (-50)+(+4) | B. | 2.7+(-4.5) | C. | (-$\frac{1}{3}$)+$\frac{2}{5}$ | D. | 0+(-$\frac{1}{3}$) |
1.下列说法正确的是( )
| A. | 任意三点可以确定一个圆 | |
| B. | 平分弦的直径垂直于弦,并且平分该弦所对的弧 | |
| C. | 同一平面内,点P到⊙O上一点的最小距离为2,最大距离为8,则该圆的半径为5 | |
| D. | 同一平面内,点P到圆心O的距离为5,且圆的半径为10,则过点P且长度为整数的弦共有5条 |
5.下列函数中,是二次函数的是( )
| A. | y=ax2+bx+c | B. | y=(x+2)(x-2)-x2 | C. | $y=\sqrt{{x^2}-2x+1}$ | D. | $y=\frac{1}{2}({x-3})x$ |
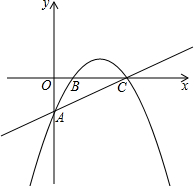 如图:在平面直角坐标系中,直线$y=\frac{1}{2}x-2$分别交x、y轴于C、A,抛物线y=-$\frac{1}{2}$x2+bx+c经过A、C两点,交x轴于另外一点B.
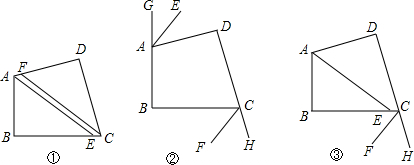
如图:在平面直角坐标系中,直线$y=\frac{1}{2}x-2$分别交x、y轴于C、A,抛物线y=-$\frac{1}{2}$x2+bx+c经过A、C两点,交x轴于另外一点B. 如图所示,AB=AC,BD=CE,AD=AE,求证:△ABE≌△ACD.
如图所示,AB=AC,BD=CE,AD=AE,求证:△ABE≌△ACD.