题目内容
在矩形ABCD中,AB=1,AD=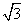 ,AF平分∠DAB,过C点作CE
,AF平分∠DAB,过C点作CE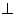 BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
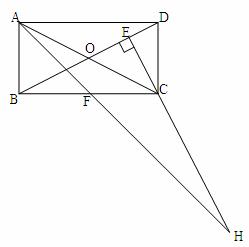
(A)1个 (B)2个 (C)3个 (D)4个
C
【解析】根据已知条件不能推出AF=FH,故①错误;
∵四边形ABCD是矩形,∴∠BAD=90°,∵AD=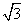 ,AB=1,∴tan∠ADB=
,AB=1,∴tan∠ADB=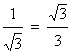 ,
,
∴∠ADB=30°,∴∠ABO=60°,∵四边形ABCD是矩形,∴AD∥BC,AC=BD,AC=2AO,BD=2BO,
∴AO=BO,∴△ABO是等边三角形,∴AB=BO,∠AOB=∠BAO=60°=∠COE,∵AF平分∠BAD,
∴∠BAF=∠DAF=45°,
∵AD∥BC,∴∠DAF=∠AFB,∴∠BAF=∠AFB,∴AB=BF,∵AB=BO,∴BF=BO,故②正确;
∵∠BAO=60°,∠BAF=45°,∴∠CAH=15°,∵CE⊥BD,∴∠ CEO=90°,∵∠EOC=60°,∴∠ECO=30°,∴∠H=∠ECO-∠CAH=30°-15°=15°=∠CAH,∴AC=CH,故③正确;
CEO=90°,∵∠EOC=60°,∴∠ECO=30°,∴∠H=∠ECO-∠CAH=30°-15°=15°=∠CAH,∴AC=CH,故③正确;
∵△AOB是等边三角形,∴AO=OB=AB,∵四边形ABCD是矩形,∴OA=OC,OB=OD,AB=CD,
∴DC=OC=OD,∵CE⊥BD,∴DE=EO= DO=
DO=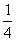 BD,∴BE=3ED,故④正确;
BD,∴BE=3ED,故④正确;
∴正确的有3个,
故选C.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 的解在数轴上表示为( )
的解在数轴上表示为( )

 =90°,则AB=
=90°,则AB= 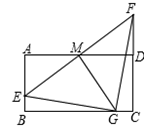

 的值为( )
的值为( )
 B.3 C.
B.3 C.
 D.2
D.2
 .则新品种花生亩产量的增长率为
.则新品种花生亩产量的增长率为 ,(1)若使
,(1)若使 成立的
成立的 值恰好有三个,则
值恰好有三个,则 = ;(2)若使
= ;(2)若使