题目内容
△ABC中,AB=AC=8,BC=14,求底角的正弦和△ABC的面积.
考点:解直角三角形
专题:
分析:作AD⊥AC,交BC于点D,将△ABC分割成两个直角三角形,进而在Rt△ABD中,由勾股定理可得AD的值,根据三角函数的定义,可得底角∠B的正弦值.
解答: 解:作AD⊥AC,交BC于点D,易得D为BC的中点,
解:作AD⊥AC,交BC于点D,易得D为BC的中点,
在Rt△ABD中,有AB=8,BD=7;
由勾股定理可得:AD=
=
,
故sinB=
=
.
S△ABC=
BC•AD=
×14×
=
.
 解:作AD⊥AC,交BC于点D,易得D为BC的中点,
解:作AD⊥AC,交BC于点D,易得D为BC的中点,在Rt△ABD中,有AB=8,BD=7;
由勾股定理可得:AD=
| 82-72 |
| 15 |
故sinB=
| AD |
| AB |
| ||
| 8 |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 8 |
7
| ||
| 8 |
点评:本题考查了锐角三角函数的定义以及等腰三角形的性质、勾股定理,要熟练掌握好边角之间的关系.

练习册系列答案
相关题目
设S=
+
+
+…+
,则4S的整数部分等于( )
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 399 |
| A、4 | B、2 | C、1 | D、0 |
 如图,反比例函数y=
如图,反比例函数y=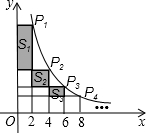 如图,在函数y=
如图,在函数y=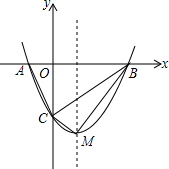 如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点.
如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点. 已知有理数a、b、c在数轴上的位置如图所示,且|a|=|b|
已知有理数a、b、c在数轴上的位置如图所示,且|a|=|b|