题目内容
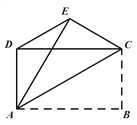
【题目】如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若![]() ,则
,则![]() 的值为( ).
的值为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】分析:根据翻折的性质可得∠BAC=∠EAC,再根据矩形的对边平行可得AB∥CD,根据两直线平行,内错角相等可得∠DAC=∠BCA,从而得到∠EAC=∠DAC,设AE与CD相交于F,根据等角对等边的性质可得AF=CF,再求出DF=EF,从而得到△ACF和△EDF相似,根据相似三角形对应边成比例求出![]() ,设DF=3x,FC=5x,在Rt△ADF中,利用勾股定理列式求出AD,再根据矩形的对边相等求出AB,然后代入进行计算即可得解.
,设DF=3x,FC=5x,在Rt△ADF中,利用勾股定理列式求出AD,再根据矩形的对边相等求出AB,然后代入进行计算即可得解.
详解:如图,
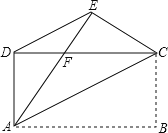
∵矩形沿直线AC折叠,点B落在点E处,
∴∠BAC=∠EAC,AE=AB=CD,
∵矩形ABCD的对边AB∥CD,
∴∠DCA=∠BAC,
∴∠EAC=∠DCA,
设AE与CD相交于F,则AF=CF,
∴AE-AF=CD-CF,
即DF=EF,
∴![]() ,
,
又∵∠AFC=∠EFD,
∴△ACF∽△EDF,
∴![]() ,
,
设DF=3x,FC=5x,则AF=5x,
在Rt△ADF中,AD=![]() ,
,
又∵AB=CD=DF+FC=3x+5x=8x,
∴![]() .
.
故选A.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
【题目】列一元一次方程解应用题:
某水果店计划购进![]() .
.![]() 两种水果,下表是
两种水果,下表是![]() .
.![]() 这两种水果的进货价格:
这两种水果的进货价格:
水果品种 |
|
|
进货价格(元 |
|
|
(1)若该水果店要花费![]() 元同时购进两种水果共
元同时购进两种水果共![]() ,则购进
,则购进![]() .
.![]() 两种水果各为多少
两种水果各为多少![]() ?
?
(2)若水果店将![]() 种水果的售价定为
种水果的售价定为![]() 元
元![]() ,要使购进的这批水果在完全售出后达到
,要使购进的这批水果在完全售出后达到![]() 的利润率,
的利润率,![]() 种水果的售价应该定为多少?
种水果的售价应该定为多少?






