题目内容
19.已知二次函数y1=x2,直线y2=2x+3,如果在-2≤x≤a内存在x的值,使得y1≤y2成立,结合函数图形求出a的取值范围.分析 首先求出两个函数的交点坐标,画出图象,利用图象即可解决问题.
解答 解:由$\left\{\begin{array}{l}{y={x}^{2}}\\{y=2x+3}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=9}\end{array}\right.$,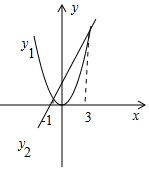
由图象可知,要使得在-2≤x≤a内存在x的值,使得y1≤y2成立,a的取值范围为a≥-1.
点评 本题考查二次函数、一次函数的图象的性质等知识,解题的关键是学会理解题意,利用图象法解决问题,属于中考常考题型.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
14.已知$\sqrt{x}$=$\frac{1-a}{2}$,$\sqrt{x+a}$-$\sqrt{x-a+2}$=-2,则a的取值范围是( )
| A. | a≤1 | B. | -1≤a≤1 | C. | a≤-1 | D. | -1≤a≤0 |
4.无论b取何值,抛物线y=a(x-b)2+b的图象顶点都在( )
| A. | x轴上 | B. | y轴上 | ||
| C. | 第一、三象限的平分线上 | D. | 第二、四象限的平分线上 |
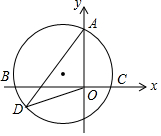 如图,在直角坐标系中,已知点A(0,4),B(-4,0),C(2,0),过A,B,C作外接圆,D为圆上一动点,求$\sqrt{5}$DO+DA的最小值.
如图,在直角坐标系中,已知点A(0,4),B(-4,0),C(2,0),过A,B,C作外接圆,D为圆上一动点,求$\sqrt{5}$DO+DA的最小值.